Funktiokaavio ja tangentit kuinka ratkaistaan. online-laskin

Ohje

Määritämme käyrän tangentin kaltevuuden pisteessä M.
Funktion y = f(x) kuvaajaa edustava käyrä on jatkuva jossain pisteen M läheisyydessä (mukaan lukien itse piste M).

Jos arvoa f’(x0) ei ole olemassa, joko tangenttia ei ole tai se kulkee pystysuunnassa. Tämän huomioon ottaen funktion derivaatan esiintyminen pisteessä x0 johtuu ei-pystysuoran tangentin olemassaolosta, joka on kosketuksessa funktion kuvaajaan pisteessä (x0, f(x0)). Tässä tapauksessa tangentin kaltevuus on yhtä suuri kuin f "(x0). Näin ollen derivaatan geometrinen merkitys tulee selväksi - tangentin kaltevuuden laskenta.

Etsi kosketuspisteen abskissan arvo, joka on merkitty kirjaimella "a". Jos se osuu yhteen annetun tangentin pisteen kanssa, "a" on sen x-koordinaatti. Määritä arvo toimintoja f(a), korvaamalla yhtälön toimintoja abskissan koko.

Määritä yhtälön ensimmäinen derivaatta toimintoja f'(x) ja korvaa siihen pisteen "a" arvo.

Otetaan yleinen tangenttiyhtälö, joka määritellään y \u003d f (a) \u003d f (a) (x - a), ja korvaa löydetyt arvot \u200b\u200b\u200b/a), f "( a) siihen.. Tuloksena graafin ratkaisu löytyy ja tangentti.

Ratkaise tehtävä eri tavalla, jos annettu tangenttipiste ei ole sama kuin tangenttipiste. Tässä tapauksessa tangenttiyhtälön numeroiden sijaan on korvattava "a". Sen jälkeen korvaa kirjainten "x" ja "y" sijasta annetun pisteen koordinaattien arvo. Ratkaise tuloksena oleva yhtälö, jossa "a" on tuntematon. Laita saatu arvo tangenttiyhtälöön.

Kirjoita yhtälö tangentille, jossa on kirjain "a", jos yhtälö on annettu tehtävän ehdossa toimintoja ja yhdensuuntaisen suoran yhtälö suhteessa haluttuun tangenttiin. Sen jälkeen tarvitset johdannaisen toimintoja pisteen "a" koordinaatille. Liitä oikea arvo tangenttiyhtälöön ja ratkaise funktio.

Olkoon annettu funktio f, jolla on jossain pisteessä x 0 äärellinen derivaatta f (x 0). Sitten pisteen (x 0; f (x 0)) läpi kulkevaa suoraa, jonka kaltevuus f '(x 0) kutsutaan tangentiksi.

Mutta mitä tapahtuu, jos derivaatta pisteessä x 0 ei ole olemassa? Vaihtoehtoja on kaksi:

1. Myöskään kaavion tangenttia ei ole olemassa. Klassinen esimerkki on funktio y = |x | pisteessä (0; 0).
2. Tangentista tulee pystysuora. Tämä pätee esimerkiksi funktiolle y = arcsin x pisteessä (1; π /2).

Tangenttiyhtälö

Mikä tahansa ei-pystysuora viiva saadaan yhtälöllä muotoa y = kx + b, missä k on kaltevuus. Tangentti ei ole poikkeus, ja sen yhtälön muodostamiseksi jossain pisteessä x 0 riittää, että tietää funktion ja derivaatan arvo tässä pisteessä.

Joten annetaan funktio y \u003d f (x), jolla on derivaatta y \u003d f '(x) segmentissä. Sitten mihin tahansa pisteeseen x 0 ∈ (a; b) voidaan piirtää tangentti tämän funktion kuvaajalle, joka saadaan yhtälöstä:

y \u003d f '(x 0) (x - x 0) + f (x 0)

Tässä f ’(x 0) on derivaatan arvo pisteessä x 0 ja f (x 0) on itse funktion arvo.

Tehtävä. Annettu funktio y = x 3 . Kirjoita yhtälö tämän funktion kaavion tangentille pisteessä x 0 = 2.

Tangenttiyhtälö: y \u003d f '(x 0) (x - x 0) + f (x 0). Piste x 0 = 2 on meille annettu, mutta arvot f (x 0) ja f '(x 0) on laskettava.

Ensin selvitetään funktion arvo. Täällä kaikki on helppoa: f (x 0) = f (2) = 2 3 = 8;
Etsitään nyt derivaatta: f '(x) \u003d (x 3) ' \u003d 3x 2;
Korvaa derivaatassa x 0 = 2: f '(x 0) = f '(2) = 3 2 2 = 12;
Joten saamme: y = 12 (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
Tämä on tangenttiyhtälö.

Tehtävä. Laadi funktion f (x) \u003d 2sin x + 5 kaavion tangentin yhtälö pisteessä x 0 \u003d π / 2.

Tällä kertaa emme kuvaa yksityiskohtaisesti jokaista toimintaa - osoitamme vain tärkeimmät vaiheet. Meillä on:

f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 \u003d 2 + 5 \u003d 7;
f '(x) \u003d (2sin x + 5) ' \u003d 2cos x;
f '(x 0) \u003d f '(π / 2) \u003d 2cos (π / 2) \u003d 0;

Tangenttiyhtälö:

y = 0 (x − π /2) + 7 ⇒ y = 7

Jälkimmäisessä tapauksessa viiva osoittautui vaakasuoraksi, koska sen kaltevuus k = 0. Siinä ei ole mitään vikaa - törmäsimme juuri ääripisteeseen.

Y \u003d f (x) ja jos tässä vaiheessa voidaan piirtää funktiokaavioon tangentti, joka ei ole kohtisuorassa x-akselia vastaan, niin tangentin kaltevuus on f "(a). Olemme jo käyttäneet tätä useita Esimerkiksi §:ssä 33 todettiin, että funktion y \u003d sin x (sinimuoto) kuvaaja origossa muodostaa 45° kulman abskissa-akselin (tarkemmin sanottuna kaavion tangentin kanssa origo muodostaa 45° kulman x-akselin positiivisen suunnan kanssa), ja esimerkissä 5 § 33 pisteet löydettiin annetulla aikataululla toimintoja, jossa tangentti on yhdensuuntainen x-akselin kanssa. §:n 33 esimerkissä 2 laadittiin yhtälö funktion y \u003d x 2 kaavion tangentille pisteessä x \u003d 1 (tarkemmin pisteessä (1; 1), mutta useammin vain abskissan arvo on osoitettu olettaen, että jos abskissan arvo tunnetaan, niin ordinaatan arvo saadaan yhtälöstä y = f(x)). Tässä osiossa kehitämme algoritmin minkä tahansa funktion kaavion tangentin yhtälön laatimiseksi.

Olkoon funktio y \u003d f (x) ja piste M (a; f (a)) annettu, ja tiedetään myös, että f "(a) on olemassa. Muodostetaan kaavion tangentin yhtälö annettu funktio tietyssä pisteessä. Tämä yhtälö on kuin minkä tahansa suoran yhtälö, ei yhdensuuntainen y-akselin kanssa, on muotoa y = kx + m, joten tehtävänä on löytää kertoimien k arvot ja m.

Kaltevuuden k kanssa ei ole ongelmia: tiedämme, että k \u003d f "(a). M:n arvon laskemiseksi käytämme sitä tosiasiaa, että haluttu suora kulkee pisteen M kautta (a; f (a)). Tämä tarkoittaa, että jos korvaamme koordinaattipisteet M suoran yhtälöön, saadaan oikea yhtälö: f (a) \u003d ka + m, josta saamme tulokseksi m \u003d f (a) - ka.
On vielä korvattava valaskertoimien löydetyt arvot yhtälö suoraan:

Olemme saaneet funktion y \u003d f (x) kaavion tangentin yhtälön pisteessä x \u003d a.
Jos vaikkapa
Korvaamalla yhtälössä (1) löydetyt arvot a \u003d 1, f (a) \u003d 1 f "(a) \u003d 2, saamme: y \u003d 1 + 2 (xf), eli y \u003d 2x -1.
Vertaa tätä tulosta 33 §:n esimerkissä 2 saatuun tulokseen. Luonnollisesti kävi samoin.
Muodostetaan funktion y \u003d tg x kaavion tangentin yhtälö origossa. Meillä on: siten cos xf "(0) = 1. Korvaamalla löydetyt arvot a \u003d 0, f (a) \u003d 0, f "(a) \u003d 1 yhtälöön (1), saamme: y \u003d x .
Tästä syystä piirsimme tangentoidin § 15:ssä (katso kuva 62) origon läpi 45°:n kulmassa abskissa-akseliin nähden.
Näiden melko yksinkertaisten esimerkkien ratkaisemiseksi käytimme itse asiassa tiettyä algoritmia, joka on upotettu kaavaan (1). Tehdään tästä algoritmista selkeä.

ALGORITMI KAAVION TANGENTIN FUNKTION YHTÄLÖN MUODOSTAMISESTA y \u003d f (x)

1) Merkitse kosketuspisteen abskissa kirjaimella a.
2) Laske 1 (a).
3) Etsi f "(x) ja laske f" (a).
4) Korvaa löydetyt luvut a, f(a), (a) kaavaan (1).

Esimerkki 1 Kirjoita yhtälö funktion kaavion tangentille pisteessä x = 1.
Käytetään algoritmia ottaen huomioon se tässä esimerkissä

Kuvassa 126 näyttää hyperbelin, muodostetaan suora y \u003d 2x.
Piirustus vahvistaa annetut laskelmat: todellakin suora y \u003d 2-x koskettaa hyperbolia pisteessä (1; 1).

Vastaus: y \u003d 2-x.
Esimerkki 2 Piirrä tangentti funktion kuvaajalle niin, että se on yhdensuuntainen suoran y \u003d 4x - 5 kanssa.
Tarkennamme ongelman muotoilua. Vaatimus "piirtää tangentti" tarkoittaa yleensä "tee yhtälö tangentille". Tämä on loogista, koska jos henkilö pystyi muodostamaan yhtälön tangentille, hänellä ei todennäköisesti ole vaikeuksia rakentaa suoraa koordinaattitasolle sen yhtälön mukaisesti.
Käytetään algoritmia tangenttiyhtälön laatimiseen, koska tässä esimerkissä, mutta toisin kuin edellisessä esimerkissä, tässä on epäselvyyttä: tangentin pisteen abskissaa ei ole nimenomaisesti osoitettu.
Aloitetaan puhuminen näin. Halutun tangentin on oltava yhdensuuntainen suoran y \u003d 4x-5 kanssa. Kaksi suoraa ovat yhdensuuntaisia ​​silloin ja vain, jos niiden kaltevuus on yhtä suuri. Tämä tarkoittaa, että tangentin kaltevuuden on oltava yhtä suuri kuin annetun suoran kaltevuus: Siten voimme löytää a:n arvon yhtälöstä f "(a) \u003d 4.
Meillä on:
Yhtälöstä Joten on olemassa kaksi tangenttia, jotka täyttävät ongelman ehdot: yksi pisteessä, jonka abskissa on 2, toinen pisteessä, jonka abskissa on -2.
Nyt voit toimia algoritmin mukaan.

Esimerkki 3 Piirrä pisteestä (0; 1) tangentti funktion kuvaajalle
Käytetään algoritmia tangenttiyhtälön laatimiseen ottaen huomioon, että tässä esimerkissä Huomaa, että tässä, kuten esimerkissä 2, tangentin pisteen abskissaa ei ole erikseen ilmoitettu. Toimimme kuitenkin algoritmin mukaan.

Ehdon mukaan tangentti kulkee pisteen (0; 1) läpi. Korvaamalla yhtälöön (2) arvot x = 0, y = 1, saadaan:
Kuten näet, tässä esimerkissä onnistuimme löytämään kosketuspisteen abskissan vasta algoritmin neljännessä vaiheessa. Korvaamalla arvon a \u003d 4 yhtälöön (2), saamme:

Kuvassa 127 esittää geometrisen kuvan tarkastelusta esimerkistä: funktion kaavio

Pykälässä 32 totesimme, että funktiolle y = f(x), jolla on derivaatta kiinteässä pisteessä x, likimääräinen yhtälö pätee:

Lisäpäättelyn helpottamiseksi muutamme merkintää: x:n sijaan kirjoitamme a, sen sijaan kirjoitamme x ja vastaavasti kirjoitamme sen sijaan x-a. Sitten yllä kirjoitettu likimääräinen yhtäläisyys saa muotoa:

Katso nyt kuva. 128. Funktion y \u003d f (x) kuvaajalle piirretään tangentti pisteessä M (a; f (a)). Merkitty piste x x-akselilla lähellä a:ta. On selvää, että f(x) on funktion kaavion ordinatta määritetyssä pisteessä x. Ja mikä on f (a) + f "(a) (x-a)? Tämä on samaa pistettä x vastaavan tangentin ordinaatti - katso kaava (1). Mitä likimääräinen yhtäläisyys (3) tarkoittaa? lasketaan funktion likimääräinen arvo, otetaan tangenttiordinaatin arvo.

Esimerkki 4 Etsi numeerisen lausekkeen likimääräinen arvo 1.02 7 .
Puhumme funktion y \u003d x 7 arvon löytämisestä pisteessä x \u003d 1,02. Käytämme kaavaa (3) ottaen sen huomioon tässä esimerkissä
Tuloksena saamme:

Jos käytämme laskinta, saamme: 1.02 7 = 1.148685667...
Kuten näet, likimääräinen tarkkuus on melko hyväksyttävä.
Vastaus: 1,02 7 =1,14.

A.G. Mordkovich-algebra, luokka 10

Kalenteri-teemaattinen suunnittelu matematiikassa, video- matematiikassa verkossa, matematiikka koulussa lataa

Tangentti on suora viiva , joka koskettaa funktion kuvaajaa yhdessä pisteessä ja jonka kaikki pisteet ovat pienimmällä etäisyydellä funktion kuvaajasta. Siksi tangentti kulkee tangentin kautta funktiokaavioon tietyssä kulmassa, ja useat tangentit eivät voi kulkea tangentin läpi eri kulmissa. Funktion kaavion tangenttiyhtälöt ja normaalin yhtälöt laaditaan derivaatta käyttäen.

Tangenttiyhtälö johdetaan suorasta yhtälöstä .

Johdamme tangentin yhtälön ja sitten funktion kaavion normaalin yhtälön.

y = kx + b .

Hänessä k- kulmakerroin.

Täältä saamme seuraavan merkinnän:

y - y 0 = k(x - x 0 ) .

Johdannainen arvo f "(x 0 ) toimintoja y = f(x) pisteessä x0 yhtä suuri kuin kaltevuus k=tg φ tangentti pisteen läpi piirretyn funktion kuvaajalle M0 (x 0 , y 0 ) , missä y0 = f(x 0 ) . Tämä on mitä johdannaisen geometrinen merkitys .

Siten voimme korvata k päällä f "(x 0 ) ja hanki seuraavat funktion kaavion tangentin yhtälö :

y - y 0 = f "(x 0 )(x - x 0 ) .

Tehtävissä funktion kaavion tangentin yhtälön laatimiseksi (ja siirrymme niihin pian) on saatava yllä olevasta kaavasta saatu yhtälö suoran suoran yleinen yhtälö. Tätä varten sinun on siirrettävä kaikki kirjaimet ja numerot yhtälön vasemmalle puolelle ja jätettävä nolla oikealle puolelle.

Nyt normaalista yhtälöstä. Normaali on suora viiva, joka kulkee tangenttia vastaan ​​kohtisuorassa olevan funktion kuvaajan tangenttipisteen kautta. Normaali yhtälö :

(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0

Ensimmäisen esimerkin lämmittämiseksi sinua pyydetään ratkaisemaan se itse ja katsomaan sitten ratkaisua. On syytä toivoa, että tämä tehtävä ei ole "kylmä suihku" lukijoillemme.

Esimerkki 0. Laadi tangentin yhtälö ja normaalin yhtälö funktion kuvaajalle pisteessä M (1, 1) .

Esimerkki 1 Muodosta tangentin yhtälö ja normaalin yhtälö funktion kuvaajaan jos kosketuspisteen abskissa on .

Etsitään funktion derivaatta:

Nyt meillä on kaikki, mikä on korvattava teoreettisessa viitteessä annettuun merkintään tangenttiyhtälön saamiseksi. Saamme

Tässä esimerkissä olimme onnekkaita: kaltevuus osoittautui nollaksi, joten yhtälöä ei tarvinnut erikseen viedä yleiseen muotoon. Nyt voimme kirjoittaa normaaliyhtälön:

Alla olevassa kuvassa: funktion kuvaaja viininpunaisella, tangentti vihreällä, normaali oranssilla.

Seuraava esimerkki ei myöskään ole monimutkainen: funktio, kuten edellisessä, on myös polynomi, mutta kulmakerroin ei ole yhtä suuri kuin nolla, joten lisätään vielä yksi askel - tuo yhtälö yleiseen muotoon.

Esimerkki 2

Ratkaisu. Etsitään kosketuspisteen ordinaatat:

Etsitään funktion derivaatta:

.

Etsitään derivaatan arvo kosketuspisteessä, eli tangentin kaltevuus:

Korvaamme kaikki saadut tiedot "tyhjäksi kaavaksi" ja saamme tangenttiyhtälön:

Tuomme yhtälön yleiseen muotoon (keräämme kaikki kirjaimet ja numerot paitsi nolla vasemmalle puolelle ja jätämme nollan oikealle):

Muodostamme normaalin yhtälön:

Esimerkki 3 Muodosta tangentin yhtälö ja normaalin yhtälö funktion kuvaajaan, jos kosketuspisteen abskissa on .

Ratkaisu. Etsitään kosketuspisteen ordinaatat:

Etsitään funktion derivaatta:

.

Etsitään derivaatan arvo kosketuspisteessä, eli tangentin kaltevuus:

.

Löydämme tangentin yhtälön:

Ennen kuin saat yhtälön yleiseen muotoon, sinun on "yhdistettävä" sitä hieman: kerrotaan termi kerrallaan 4:llä. Teemme näin ja tuomme yhtälön yleiseen muotoon:

Muodostamme normaalin yhtälön:

Esimerkki 4 Muodosta tangentin yhtälö ja normaalin yhtälö funktion kuvaajaan, jos kosketuspisteen abskissa on .

Ratkaisu. Etsitään kosketuspisteen ordinaatat:

.

Etsitään funktion derivaatta:

Etsitään derivaatan arvo kosketuspisteessä, eli tangentin kaltevuus:

.

Saamme tangenttiyhtälön:

Tuomme yhtälön yleiseen muotoon:

Muodostamme normaalin yhtälön:

Yleinen virhe kirjoitettaessa tangentti- ja normaaliyhtälöitä on olla huomaamatta, että esimerkissä annettu funktio on monimutkainen, ja laskea sen derivaatta yksinkertaisen funktion derivaatana. Seuraavat esimerkit ovat jo monimutkaiset toiminnot(vastaava oppitunti avautuu uuteen ikkunaan).

Esimerkki 5 Muodosta tangentin yhtälö ja normaalin yhtälö funktion kuvaajaan, jos kosketuspisteen abskissa on .

Ratkaisu. Etsitään kosketuspisteen ordinaatat:

Huomio! Tämä funktio on monimutkainen, koska tangentin argumentti (2 x) on itse toiminto. Siksi löydämme funktion derivaatan kompleksisen funktion derivaatana.

Artikkelissa selitetään yksityiskohtaisesti määritelmät, derivaatan geometrinen merkitys graafisella merkinnällä. Tangenttiviivan yhtälöä tarkastellaan esimerkein, 2. kertaluvun käyrien tangentin yhtälöt löytyvät.

Yandex.RTB R-A-339285-1 Määritelmä 1

Suoran y \u003d k x + b kaltevuuskulmaa kutsutaan kulmaksi α, joka mitataan x-akselin positiivisesta suunnasta suoralle y \u003d k x + b positiivisessa suunnassa.

Kuvassa härän suunta on merkitty vihreällä nuolella ja vihreällä kaarella ja kaltevuuskulma punaisella kaarella. Sininen viiva viittaa suoraan viivaan.

Määritelmä 2

Suoran y \u003d k x + b kaltevuutta kutsutaan numeeriseksi kertoimeksi k.

Kaltevuus on yhtä suuri kuin suoran kaltevuus, toisin sanoen k = t g α .

• Suoran kaltevuus on 0 vain, kun o x on yhdensuuntainen ja kaltevuus on nolla, koska nollan tangentti on 0. Joten yhtälön muoto on y = b.
• Jos suoran kaltevuuskulma y = k x + b on terävä, niin ehdot ovat 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, ja kaaviossa on kasvua.
• Jos α \u003d π 2, niin suoran sijainti on kohtisuorassa x:n kanssa. Tasa-arvo määritellään yhtälöllä x = c, jossa c on reaaliluku.
• Jos suoran kaltevuuskulma y = k x + b on tylppä, niin se vastaa ehtoja π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Sekantti on suora, joka kulkee funktion f (x) 2 pisteen kautta. Toisin sanoen sekantti on suora viiva, joka kulkee minkä tahansa kahden pisteen läpi tietyn funktion kaaviossa.

Kuvasta näkyy, että A B on sekantti ja f (x) on musta käyrä, α on punainen kaari, joka osoittaa sekantin kaltevuuskulman.

Kun suoran kaltevuus on yhtä suuri kuin kaltevuuskulman tangentti, on selvää, että suorakulmaisen kolmion A B C tangentti löytyy suhteessa viereisen kolmion vastakkaiseen haaraan.

Määritelmä 4

Saamme kaavan lomakkeen sekantin löytämiseksi:

k = tg α = BCAC = f (x B) - fx A x B - x A , missä pisteiden A ja B abskissat ovat arvot x A , x B ja f (x A) , f (x B) ovat arvofunktiot näissä kohdissa.

Ilmeisesti sekantin kaltevuus määritellään yhtälöllä k \u003d f (x B) - f (x A) x B - x A tai k \u003d f (x A) - f (x B) x A - x B, ja yhtälö on kirjoitettava muodossa y = f (x B) - f (x A) x B - x A x - x A + f (x A) tai
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Sekantti jakaa kaavion visuaalisesti kolmeen osaan: pisteen A vasemmalla puolella, pisteestä A paikkaan B, pisteen B oikealla puolella. Alla olevasta kuvasta näkyy, että on kolme sekanttia, joita pidetään samanlaisina, eli ne ovat asettaa käyttämällä samanlaista yhtälöä.

Määritelmän mukaan on selvää, että viiva ja sen sekantti ovat tässä tapauksessa samat.

Sekantti voi leikata tietyn funktion kuvaajan useita kertoja. Jos sekantille on yhtälö muotoa y \u003d 0, niin siniaallon leikkauspisteiden määrä on ääretön.

Määritelmä 5

Tangentti funktion f (x) kuvaajalle pisteessä x 0 ; f (x 0) kutsutaan suoraksi, joka kulkee tietyn pisteen x 0 kautta; f (x 0) , jossa on segmentti, jolla on useita x-arvoja lähellä x 0 -arvoa.

Esimerkki 1

Katsotaanpa tarkemmin alla olevaa esimerkkiä. Tällöin voidaan nähdä, että funktion y = x + 1 antaman suoran katsotaan olevan tangentti y = 2 x pisteessä, jossa on koordinaatit (1 ; 2) . Selvyyden vuoksi on tarpeen tarkastella kaavioita, joiden arvot ovat lähellä (1; 2). Funktio y = 2 x on merkitty mustalla, sininen viiva on tangentti, punainen piste on leikkauspiste.

Ilmeisesti y \u003d 2 x sulautuu riviin y \u003d x + 1.

Tangentin määrittämiseksi tarkastellaan tangentin A B käyttäytymistä, kun piste B lähestyy äärettömästi pistettä A. Selvyyden vuoksi esitetään kuva.

Sekantti A B, joka on merkitty sinisellä viivalla, pyrkii itse tangentin asentoon, ja sekantin kaltevuuskulma α alkaa taipua itse tangentin kaltevuuskulmaan α x.

Määritelmä 6

Funktion y \u003d f (x) kaavion tangentti pisteessä A on sekantin A B raja-asema kohdassa B, joka pyrkii A:han, eli B → A.

Nyt tarkastellaan funktion derivaatan geometrista merkitystä pisteessä.

Siirrytään tarkastelemaan funktion f (x) sekanttia AB, jossa A ja B koordinaatteilla x 0, f (x 0) ja x 0 + ∆ x, f (x 0 + ∆ x) ja ∆ x on ilmaistaan ​​argumentin lisäyksenä. Nyt funktio saa muotoa ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Selvyyden vuoksi otetaan kuva esimerkkinä.

Tarkastellaan tuloksena olevaa suorakulmaista kolmiota A B C. Käytämme ratkaisun tangentin määritelmää, eli saamme suhteen ∆ y ∆ x = t g α . Tangentin määritelmästä seuraa, että lim ∆ x → 0 ∆ y ∆ x = t g α x . Derivaatasäännön mukaan pisteessä derivaatta f (x) pisteessä x 0 kutsutaan funktion inkrementin ja argumentin inkrementin suhteen rajaksi, missä ∆ x → 0, niin merkitty f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Tästä seuraa, että f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, missä k x on merkitty tangentin kulmakertoimeksi.

Eli saamme, että f ' (x) voi olla pisteessä x 0 ja kuten funktion annetun kaavion tangentti kosketuspisteessä, joka on yhtä suuri kuin x 0, f 0 (x 0) , jossa arvo tangentin kulmakerroin pisteessä on yhtä suuri kuin derivaatta pisteessä x 0 . Sitten saadaan, että k x = f "(x 0) .

Funktion derivaatan geometrinen merkitys pisteessä on, että on annettu käsite graafin tangentin olemassaolosta samassa pisteessä.

Minkä tahansa suoran yhtälön kirjoittamiseksi tasoon tarvitaan kaltevuus sen pisteen kanssa, jonka läpi se kulkee. Sen merkintä on x 0 risteyksessä.

Funktion y \u003d f (x) kaavion tangentin yhtälö pisteessä x 0, f 0 (x 0) on muodossa y \u003d f "(x 0) x - x 0 + f (x) 0) .

Se tarkoittaa, että derivaatan f "(x 0) lopullinen arvo voi määrittää tangentin sijainnin, eli pystysuoraan ehdolla lim x → x 0 + 0 f" (x) = ∞ ja lim x → x 0 - 0 f "(x ) = ∞ tai poissaolo ollenkaan ehdolla lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f "(x) .

Tangentin sijainti riippuu sen kulmakertoimen arvosta kx \u003d f "(x 0). Kun se on yhdensuuntainen x-akselin kanssa, saadaan, että kk \u003d 0, kun se on yhdensuuntainen noin y - kx \u003d ∞ kanssa, ja tangenttiyhtälön muoto x \u003d x 0 kasvaa kun kx > 0, pienenee kun kx< 0 .

Esimerkki 2

Laadi funktion y \u003d ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 kaavion tangentin yhtälö pisteessä, jonka koordinaatit (1; 3) kulman määritelmällä kaltevuus.

Ratkaisu

Oletuksena on, että funktio on määritelty kaikille reaaliluvuille. Saamme, että ehdon (1 ; 3) määrittelemä piste on kosketuspiste, jolloin x 0 = - 1 , f (x 0) = - 3 .

Derivaata on löydettävä pisteestä, jonka arvo on -1. Me ymmärrämme sen

y "= ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" == ex + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = ex + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Arvo f ’ (x) kosketuspisteessä on tangentin kulmakerroin, joka on yhtä suuri kuin kulman tangentti.

Sitten k x = t g α x = y "(x 0) = 3 3

Tästä seuraa, että α x = a r c t g 3 3 = π 6

Vastaus: tangenttiyhtälö saa muodon

y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3

Selvyyden vuoksi annamme esimerkin graafisessa kuvassa.

Mustaa väriä käytetään alkuperäisen funktion kuvaajana, sininen väri on tangenttikuva, punainen piste on kosketuspiste. Oikealla oleva kuva näyttää suurennettuna.

Esimerkki 3

Selvitä tietyn funktion kaavion tangentin olemassaolo
y = 3 x - 1 5 + 1 pisteessä, jonka koordinaatit (1 ; 1) . Kirjoita yhtälö ja määritä kaltevuuskulma.

Ratkaisu

Oletuksena meillä on, että annetun funktion toimialue on kaikkien reaalilukujen joukko.

Siirrytään johdannaisen etsimiseen

y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Jos x 0 = 1, niin f' (x) ei ole määritelty, vaan rajat kirjoitetaan muodossa lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + ∞ ja lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , mikä tarkoittaa pystytangentin olemassaoloa kohdassa kohta (1 ; 1) .

Vastaus: yhtälö on muodossa x \u003d 1, jossa kaltevuuskulma on yhtä suuri kuin π 2.

Piirretään se selvyyden vuoksi.

Esimerkki 4

Etsi funktiokuvaajan pisteet y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , missä

1. Tangenttia ei ole olemassa;
2. Tangentti on yhdensuuntainen x:n kanssa;
3. Tangentti on yhdensuuntainen suoran y = 8 5 x + 4 kanssa.

Ratkaisu

On tarpeen kiinnittää huomiota määrittelyalueeseen. Oletuksena on, että funktio on määritelty kaikkien reaalilukujen joukossa. Laajenna moduulia ja ratkaise järjestelmä intervalleilla x ∈ - ∞ ; 2 ja [-2; +∞) . Me ymmärrämme sen

y = -1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)

Toiminto on eriytettävä. Meillä se on

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35), x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)

Kun x = - 2, niin derivaatta ei ole olemassa, koska yksipuoliset rajat eivät ole samat tässä pisteessä:

lim x → - 2 - 0 y "(x) = raja x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = raja x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Laskemme funktion arvon pisteessä x \u003d - 2, josta saamme sen

1. y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, eli tangentti kohtaa (- 2; - 2) ei ole olemassa.
2. Tangentti on yhdensuuntainen x:n kanssa, kun kulmakerroin on nolla. Sitten kx \u003d tg α x \u003d f "(x 0). Eli on tarpeen löytää sellaisen x:n arvot, kun funktion derivaatta muuttaa sen nollaksi. Eli arvot f '(x) ja ovat kosketuspisteitä, joissa tangentti on yhdensuuntainen x:n kanssa.

Kun x ∈ - ∞ ; -2, sitten -1 5 (x 2 + 12 x + 35) = 0, ja x ∈ (- 2 ; + ∞) saa 1 5 (x 2 - 4 x + 3) = 0 .

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Laskemme funktion vastaavat arvot

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Tästä syystä - 5; 8 5, - 4; 4 3, 1; 85, 3; 4 3 katsotaan funktion kaavion halutuiksi pisteiksi.

Harkitse ratkaisun graafista esitystä.

Musta viiva on funktion kaavio, punaiset pisteet kosketuspisteitä.

1. Kun viivat ovat yhdensuuntaiset, kaltevuus on yhtä suuri. Sitten on etsittävä funktion kaavion pisteet, joissa kaltevuus on yhtä suuri kuin arvo 8 5 . Tätä varten sinun on ratkaistava yhtälö, jonka muoto on y "(x) = 8 5. Sitten, jos x ∈ - ∞; - 2, saamme, että - 1 5 (x 2 + 12 x + 35) = 8 5, ja jos x ∈ ( - 2 ; + ∞) , niin 1 5 (x 2 - 4 x + 3) = 8 5 .

Ensimmäisellä yhtälöllä ei ole juuria, koska diskriminantti on pienempi kuin nolla. Kirjoitetaan se ylös

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Toisella yhtälöllä on siis kaksi todellista juuria

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Siirrytään funktion arvojen etsimiseen. Me ymmärrämme sen

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Pisteet arvoilla -1 ; 4 15, 5; 8 3 ovat pisteitä, joissa tangentit ovat yhdensuuntaiset suoran y = 8 5 x + 4 kanssa.

Vastaus: musta viiva - funktion kaavio, punainen viiva - kaavio y \u003d 8 5 x + 4, sininen viiva - tangentit pisteissä - 1; 4 15, 5; 8 3 .

Tietyille funktioille on mahdollista olla ääretön määrä tangentteja.

Esimerkki 5

Kirjoita funktion y = 3 cos 3 2 x - π 4 - 1 3 kaikkien käytettävissä olevien tangenttien yhtälöt, jotka ovat kohtisuorassa suoraa y = - 2 x + 1 2 vastaan.

Ratkaisu

Tangenttiyhtälön laatimiseksi on tarpeen löytää tangentin pisteen kerroin ja koordinaatit suorien kohtisuoran ehdon perusteella. Määritelmä kuulostaa tältä: suorien kohtisuorassa olevien kaltevuuden tulo on yhtä suuri kuin -1, eli se kirjoitetaan muodossa k x · k ⊥ = - 1. Ehdosta saadaan, että kaltevuus on kohtisuorassa suoraa vastaan ​​ja on yhtä kuin k ⊥ = - 2, jolloin k x = - 1 k ⊥ = - 1 - 2 = 1 2 .

Nyt meidän on löydettävä kosketuspisteiden koordinaatit. Sinun on löydettävä x, jonka jälkeen sen arvo tietylle funktiolle. Huomaa, että derivaatan geometrisesta merkityksestä pisteessä
x 0 saamme, että k x \u003d y "(x 0) . Tästä yhtälöstä löydämme kosketuspisteiden x-arvot.

Me ymmärrämme sen

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 \u003d - 9 2 sin 3 2 x 0 - π 4 ⇒ kx \u003d y "(x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ 0 sin -3 π 2 x 4 = - 1 9

Tätä trigonometristä yhtälöä käytetään kosketuspisteiden ordinaattien laskemiseen.

3 2 x 0 - π 4 = arc sin - 1 9 + 2 πk tai 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk tai 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - arc sin 1 9 + 2 πk tai x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z on kokonaislukujen joukko.

Löytyi x kontaktipistettä. Nyt sinun on siirryttävä etsimään y-arvoja:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 tai y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 tai y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 tai y 0 = - 4 5 + 1 3

Tästä saadaan, että 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + arc sin 1 9 + 2 πk ; - 4 5 + 1 3 ovat kosketuspisteitä.

Vastaus: tarvittavat yhtälöt kirjoitetaan muodossa

y = 1 2 x - 2 3 π 4 - kaari sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + kaarisin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Visuaalista esitystä varten harkitse koordinaattiviivan funktiota ja tangenttia.

Kuvasta näkyy, että funktion sijainti on intervallilla [-10; 10] , jossa musta viiva on funktion kuvaaja, siniset viivat ovat tangentteja, jotka ovat kohtisuorassa annettua muotoa y = - 2 x + 1 2 olevaa suoraa vastaan. Punaiset pisteet ovat kosketuspisteitä.

Toisen asteen käyrien kanoniset yhtälöt eivät ole yksiarvoisia funktioita. Niiden tangenttiyhtälöt kootaan tunnettujen kaavioiden mukaisesti.

Tangentti ympyrään

Ympyrän asettaminen pisteeseen x c e n t e r ; y c e n t e r ja säde R, käytetään kaavaa x - x c e n t e r 2 + y - y c e n t e r 2 = R 2.

Tämä yhtäläisyys voidaan kirjoittaa kahden funktion liitoksi:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Ensimmäinen toiminto on ylhäällä ja toinen alhaalla, kuten kuvassa näkyy.

Piirtää ympyrän yhtälö pisteessä x 0 ; y 0 , joka sijaitsee ylemmässä tai alemmassa puoliympyrässä, sinun tulee löytää funktiokaavion yhtälö muotoa y \u003d R 2 - x - xcenter 2 + ycenter tai y \u003d - R 2 - x - xcenter 2 + ycenter määritetyssä kohdassa.

Kun pisteissä x c e n t e r ; y c e n t e r + R ja x c e n t e r; y c e n t e r - R tangentit voidaan antaa yhtälöillä y = y c e n t e r + R ja y = y c e n t e r - R ja pisteissä x c e n t e r + R ; y c e n t e r ja
x c e n t e r-R; y c e n t e r on yhdensuuntainen y:n ympäri, jolloin saadaan yhtälöt muotoa x = x c e n t e r + R ja x = x c e n t e r - R .

Tangentti ellipsille

Kun ellipsi on keskitetty kohtaan x c e n t e r ; y c e n t e r puoliakseleilla a ja b , niin se voidaan antaa yhtälöllä x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .

Ellipsi ja ympyrä voidaan merkitä yhdistämällä kaksi funktiota, nimittäin ylempi ja alempi puoliellipsi. Sitten saamme sen

y = b a a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a a 2 - (x - x c e n t e r) 2 + y c e n t e r

Jos tangentit sijaitsevat ellipsin kärjessä, ne ovat yhdensuuntaisia ​​x:n tai y:n suhteen. Selvyyden vuoksi harkitse alla olevaa kuvaa.

Esimerkki 6

Kirjoita ellipsin tangentin yhtälö x - 3 2 4 + y - 5 2 25 = 1 pisteissä, joiden x arvo on yhtä suuri kuin x = 2 .

Ratkaisu

On tarpeen löytää kosketuspisteet, jotka vastaavat arvoa x = 2. Teemme korvauksen olemassa olevaan ellipsin yhtälöön ja saamme sen

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Sitten 2; 5 3 2 + 5 ja 2; - 5 3 2 + 5 ovat tangenttipisteitä, jotka kuuluvat ylempään ja alempaan puoliellipsiin.

Jatketaan ellipsin yhtälön löytämiseen ja ratkaisemiseen y:n suhteen. Me ymmärrämme sen

x - 3 2 4 + y - 5 2 25 = 1 v - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 v - 5 = ± 5 1 - x - 3 2 4 v = 5 ± 5 2 4 - x - 3 2

On selvää, että ylempi puoliellipsi määritellään muotoa y = 5 + 5 2 4 - x - 3 2 olevalla funktiolla ja alempi y = 5 - 5 2 4 - x - 3 2 .

Käytämme standardialgoritmia muotoillaksemme funktion kaavion tangentin yhtälön pisteessä. Kirjoitamme, että ensimmäisen tangentin yhtälö pisteessä 2 ; 5 3 2 + 5 näyttää siltä

y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Saamme, että toisen tangentin yhtälö pisteen arvon kanssa
2; - 5 3 2 + 5 tulee

y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Graafisesti tangentit on merkitty seuraavasti:

Tangentti hyperbolille

Kun hyperbolilla on keskipiste pisteessä x c e n t e r ; y c e n t e r ja kärjet x c e n t e r + α ; y c e n t e r ja x c e n t e r - α ; y c e n t e r , epäyhtälö x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 on annettu, jos pisteillä x c e n t e r ; y c e n t e r + b ja x c e n t e r ; y c e n t e r - b saadaan sitten epäyhtälöstä x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hyperbola voidaan esittää muodon kahtena yhdistettynä funktiona

y = ba (x - xcenter) 2 - a 2 + ycentery = - ba (x - xcenter) 2 - a 2 + ycenter tai y = ba (x - xcenter) 2 + a 2 + ycentery = - ba (x - xcenter) ) 2 + a 2 + ycenter

Ensimmäisessä tapauksessa tangentit ovat yhdensuuntaisia ​​y:n kanssa, ja toisessa tapauksessa ne ovat yhdensuuntaisia ​​x:n kanssa.

Tästä seuraa, että hyperbolin tangentin yhtälön löytämiseksi on selvitettävä, mihin funktioon tangenttipiste kuuluu. Tämän määrittämiseksi on välttämätöntä tehdä korvaus yhtälöissä ja tarkistaa niiden identiteetti.

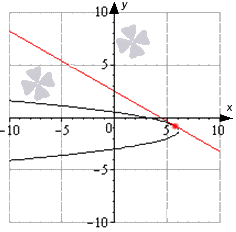
Esimerkki 7

Kirjoita hyperbolin tangentin yhtälö x - 3 2 4 - y + 3 2 9 = 1 pisteeseen 7; - 3 3 - 3 .

Ratkaisu

Hyperbolan löytämisen ratkaisun tietue on muutettava kahdella funktiolla. Me ymmärrämme sen

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 tai y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

On selvitettävä, mihin funktioon annettu piste koordinaatteilla 7 kuuluu; - 3 3 - 3 .

Ilmeisesti ensimmäisen funktion tarkistamiseksi tarvitaan y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, jolloin piste ei kuulu kuvaajaan, koska tasa-arvo ei täyty.

Toiselle funktiolle on, että y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , mikä tarkoittaa, että piste kuuluu annettuun kuvaajaan. Täältä sinun pitäisi löytää kaltevuuskerroin.

Me ymmärrämme sen

y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ kx = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Vastaus: tangenttiyhtälö voidaan esittää muodossa

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Se visualisoidaan seuraavasti:

Tangentti paraabelille

Muodostaaksesi paraabelin tangentin yhtälön y \u003d ax 2 + bx + c pisteessä x 0, y (x 0) , sinun on käytettävä standardialgoritmia, jolloin yhtälö on muodossa y \u003d y " (x 0) x - x 0 + y ( x 0) Tällainen tangentti kärjessä on x:n suuntainen.

Paraabeli x = a y 2 + b y + c tulisi määritellä kahden funktion liitoksi. Siksi meidän on ratkaistava yhtälö y:lle. Me ymmärrämme sen

x = ay 2 + by + c ⇔ ay 2 + by + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 ay = - b - b 2 - 4 a (c - x) 2 a

Piirretään se seuraavasti:

Selvittääksesi, kuuluuko piste x 0, y (x 0) funktioon, seuraa varovasti standardialgoritmia. Tällainen tangentti on yhdensuuntainen y:n kanssa paraabelin suhteen.

Esimerkki 8

Kirjoita kaavion tangentin yhtälö x - 2 y 2 - 5 y + 3, kun tangentin kaltevuus on 150 °.

Ratkaisu

Aloitamme ratkaisun esittämällä paraabelin kahtena funktiona. Me ymmärrämme sen

2 v 2 - 5 v + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 xy = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Kulmakertoimen arvo on yhtä suuri kuin derivaatan arvo tämän funktion pisteessä x 0 ja on yhtä suuri kuin kulmakertoimen tangentti.

Saamme:

k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3

Tästä määritämme kosketuspisteiden x:n arvon.

Ensimmäinen funktio kirjoitetaan muodossa

y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Varsinaisia ​​juuria ei tietenkään ole, koska saimme negatiivisen arvon. Päättelemme, että tällaiselle funktiolle ei ole tangenttia, jonka kulma on 150 °.

Toinen funktio kirjoitetaan muodossa

y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Meillä on, että kosketuspisteet - 23 4 ; - 5 + 3 4 .

Vastaus: tangenttiyhtälö saa muodon

y = -1 3 x - 23 4 + - 5 + 3 4

Piirretään se seuraavasti:

Jos huomaat tekstissä virheen, korosta se ja paina Ctrl+Enter