फंक्शन ग्राफ और टैंगेंट कैसे हल करें। ऑनलाइन कैलकुलेटर

अनुदेश

हम बिंदु M पर वक्र की स्पर्शरेखा का ढलान निर्धारित करते हैं।
फ़ंक्शन y = f(x) के ग्राफ का प्रतिनिधित्व करने वाला वक्र बिंदु M के कुछ पड़ोस में निरंतर है (बिंदु M सहित)।

यदि मान f'(x0) मौजूद नहीं है, तो या तो कोई स्पर्शरेखा नहीं है, या यह लंबवत रूप से गुजरती है। इसे देखते हुए, बिंदु x0 पर फ़ंक्शन के व्युत्पन्न की उपस्थिति एक गैर-ऊर्ध्वाधर स्पर्शरेखा के अस्तित्व के कारण है जो बिंदु (x0, f(x0)) पर फ़ंक्शन के ग्राफ़ के संपर्क में है। इस मामले में, स्पर्शरेखा का ढलान f "(x0) के बराबर होगा। इस प्रकार, व्युत्पन्न का ज्यामितीय अर्थ स्पष्ट हो जाता है - स्पर्शरेखा के ढलान की गणना।

संपर्क बिंदु के भुज का मान ज्ञात कीजिए, जिसे "a" अक्षर से दर्शाया जाता है। यदि यह दिए गए स्पर्शरेखा बिंदु से मेल खाता है, तो "a" इसका x-निर्देशांक होगा। मूल्य निर्धारित करें कार्यों f(a), समीकरण में प्रतिस्थापित करना कार्योंएब्सिस्सा का आकार।

समीकरण का पहला व्युत्पन्न निर्धारित करें कार्यों f'(x) और इसमें बिंदु "a" के मान को प्रतिस्थापित करें।

सामान्य स्पर्शरेखा समीकरण लें, जिसे y \u003d f (a) \u003d f (a) (x - a) के रूप में परिभाषित किया गया है, और पाए गए मानों को a, f (a), f "( ए) इसमें। परिणामस्वरूप, ग्राफ का हल मिलेगा और स्पर्शरेखा होगा।

समस्या को अलग तरीके से हल करें यदि दिया गया स्पर्शरेखा बिंदु स्पर्शरेखा बिंदु से मेल नहीं खाता है। इस मामले में, स्पर्शरेखा समीकरण में संख्याओं के बजाय "ए" को प्रतिस्थापित करना आवश्यक है। उसके बाद, "x" और "y" अक्षरों के बजाय, दिए गए बिंदु के निर्देशांक के मान को प्रतिस्थापित करें। परिणामी समीकरण को हल करें जिसमें "ए" अज्ञात है। परिणामी मान को स्पर्शरेखा समीकरण में रखें।

"a" अक्षर वाली स्पर्श रेखा के लिए एक समीकरण लिखिए, यदि समीकरण समस्या की स्थिति में दिया गया हो कार्योंऔर वांछित स्पर्शरेखा के संबंध में एक समानांतर रेखा का समीकरण। उसके बाद, आपको एक व्युत्पन्न की आवश्यकता है कार्योंबिंदु "ए" पर समन्वय करने के लिए। उपयुक्त मान को स्पर्शरेखा समीकरण में प्लग करें और फ़ंक्शन को हल करें।

मान लीजिए कि एक फलन f दिया गया है, जिसका किसी बिंदु x 0 पर एक परिमित व्युत्पन्न f (x 0) है। तब बिंदु (x 0; f (x 0)) से गुजरने वाली रेखा, जिसका ढलान f '(x 0) है, स्पर्शरेखा कहलाती है।

लेकिन क्या होता है यदि बिंदु x 0 पर अवकलज मौजूद नहीं है? दो विकल्प हैं:

1. ग्राफ की स्पर्शरेखा भी मौजूद नहीं है। क्लासिक उदाहरण फ़ंक्शन y = |x | . है बिंदु पर (0; 0)।
2. स्पर्शरेखा लंबवत हो जाती है। यह सत्य है, उदाहरण के लिए, फलन y = arcsin x बिंदु पर (1; /2) के लिए।

स्पर्शरेखा समीकरण

कोई भी गैर-ऊर्ध्वाधर सीधी रेखा y = kx + b के रूप के समीकरण द्वारा दी जाती है, जहाँ k ढलान है। स्पर्शरेखा कोई अपवाद नहीं है, और किसी बिंदु x 0 पर इसके समीकरण की रचना करने के लिए, इस बिंदु पर फ़ंक्शन और व्युत्पन्न के मूल्य को जानना पर्याप्त है।

तो, एक फ़ंक्शन को y \u003d f (x) दिया जाता है, जिसका खंड पर व्युत्पन्न y \u003d f '(x) है। फिर किसी भी बिंदु पर x 0 (ए; बी) इस फ़ंक्शन के ग्राफ पर एक स्पर्शरेखा खींची जा सकती है, जो समीकरण द्वारा दी गई है:

y \u003d f '(x 0) (x - x 0) + f (x 0)

यहाँ f '(x 0) बिंदु x 0 पर अवकलज का मान है, और f (x 0) स्वयं फलन का मान है।

कार्य। एक फलन y = x 3 दिया गया है। इस फलन के आलेख की स्पर्श रेखा के लिए बिंदु x 0 = 2 पर एक समीकरण लिखिए।

स्पर्शरेखा समीकरण: y \u003d f '(x 0) (x - x 0) + f (x 0)। बिंदु x 0 = 2 हमें दिया गया है, लेकिन f (x 0) और f '(x 0) के मानों की गणना करनी होगी।

सबसे पहले, फ़ंक्शन का मान ज्ञात करें। यहाँ सब कुछ आसान है: f (x 0) = f (2) = 2 3 = 8;
अब आइए व्युत्पन्न खोजें: f '(x) \u003d (x 3)' \u003d 3x 2;
व्युत्पन्न x 0 = 2: f '(x 0) = f '(2) = 3 2 2 = 12;
तो हम पाते हैं: y = 12 (x - 2) + 8 = 12x - 24 + 8 = 12x - 16।
यह स्पर्शरेखा समीकरण है।

कार्य। फ़ंक्शन f (x) \u003d 2sin x + 5 के बिंदु x 0 \u003d π / 2 पर स्पर्शरेखा के समीकरण की रचना करें।

इस बार हम प्रत्येक क्रिया का विस्तार से वर्णन नहीं करेंगे - हम केवल मुख्य चरणों का संकेत देंगे। हमारे पास है:

f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 \u003d 2 + 5 \u003d 7;
f '(x) \u003d (2sin x + 5) ' \u003d 2cos x;
f '(x 0) \u003d f '(π / 2) \u003d 2cos (π / 2) \u003d 0;

स्पर्शरेखा समीकरण:

वाई = 0 (एक्स - π / 2) + 7 ⇒ वाई = 7

बाद के मामले में, रेखा क्षैतिज निकली, क्योंकि इसका ढलान k = 0. इसमें कुछ भी गलत नहीं है - हम बस एक चरम बिंदु पर ठोकर खा गए।

Y \u003d f (x) और यदि इस बिंदु पर एक स्पर्शरेखा को फ़ंक्शन ग्राफ़ पर खींचा जा सकता है जो x-अक्ष के लंबवत नहीं है, तो स्पर्शरेखा का ढलान f "(a) है। हम पहले से ही इसका कई उपयोग कर चुके हैं समय। उदाहरण के लिए, 33 में यह स्थापित किया गया था, कि मूल पर फ़ंक्शन y \u003d sin x (साइनसॉइड) का ग्राफ एब्सिस्सा अक्ष के साथ 45 ° का कोण बनाता है (अधिक सटीक रूप से, ग्राफ पर स्पर्शरेखा मूल x अक्ष की धनात्मक दिशा के साथ 45 ° का कोण बनाता है), और उदाहरण में 33 में से 5 अंक दिए गए समय पर पाए गए कार्यों, जिसमें स्पर्शरेखा x-अक्ष के समानांतर है। 33 के उदाहरण 2 में, बिंदु x \u003d 1 (अधिक सटीक रूप से, बिंदु (1; 1) पर फ़ंक्शन y \u003d x 2 के ग्राफ के स्पर्शरेखा के लिए एक समीकरण तैयार किया गया था, लेकिन अधिक बार केवल भुज का मान इंगित किया जाता है, यह मानते हुए कि यदि भुज का मान ज्ञात है, तो कोटि का मान समीकरण y = f(x) से ज्ञात किया जा सकता है। इस खंड में, हम किसी फलन के ग्राफ़ पर स्पर्शरेखा के समीकरण को संकलित करने के लिए एक एल्गोरिथम विकसित करेंगे।

मान लें कि फ़ंक्शन y \u003d f (x) और बिंदु M (a; f (a)) दिया गया है, और यह भी ज्ञात है कि f "(a) मौजूद है। आइए हम ग्राफ के स्पर्शरेखा के समीकरण की रचना करें दिए गए बिंदु पर दिए गए फ़ंक्शन। यह समीकरण किसी भी सीधी रेखा के समीकरण की तरह है, जो y-अक्ष के समानांतर नहीं है, इसका रूप y = kx + m है, इसलिए समस्या गुणांक k के मानों को खोजने की है और एम.

ढलान k के साथ कोई समस्या नहीं है: हम जानते हैं कि k \u003d f "(a)। m के मान की गणना करने के लिए, हम इस तथ्य का उपयोग करते हैं कि वांछित रेखा बिंदु M (a; f (a)) से होकर गुजरती है। इसका मतलब यह है कि यदि हम निर्देशांक M को एक सीधी रेखा के समीकरण में प्रतिस्थापित करते हैं, तो हमें सही समानता मिलती है: f (a) \u003d ka + m, जहाँ से हम पाते हैं कि m \u003d f (a) - ka।
यह व्हेल गुणांक के पाए गए मूल्यों को प्रतिस्थापित करने के लिए बनी हुई है समीकरणसीधा:

हमने बिंदु x \u003d a पर फ़ंक्शन y \u003d f (x) के ग्राफ के स्पर्शरेखा का समीकरण प्राप्त किया है।
अगर कहें,
समीकरण (1) में पाया गया मान a \u003d 1, f (a) \u003d 1 f "(a) \u003d 2, हमें मिलता है: y \u003d 1 + 2 (xf), यानी y \u003d 2x -1.
इस परिणाम की तुलना 33 के उदाहरण 2 में प्राप्त परिणाम से करें। स्वाभाविक रूप से, वही हुआ।
आइए हम फंक्शन y \u003d tg x के मूल में ग्राफ़ के स्पर्शरेखा के समीकरण की रचना करें। हमारे पास है: इसलिए cos xf "(0) = 1. पाए गए मानों को a \u003d 0, f (a) \u003d 0, f "(a) \u003d 1 को समीकरण (1) में प्रतिस्थापित करने पर, हमें मिलता है: y \u003d x .
यही कारण है कि हमने 15 में स्पर्शरेखा खींची (चित्र 62 देखें) मूल के माध्यम से 45 ° के कोण पर भुज अक्ष पर।
इन सरल उदाहरणों को हल करते हुए, हमने वास्तव में एक निश्चित एल्गोरिथम का उपयोग किया, जो सूत्र (1) में अंतर्निहित है। आइए इस एल्गोरिथम को स्पष्ट करें।

ग्राफ़ y \u003d f (x) के लिए स्पर्शरेखा फ़ंक्शन के समीकरण की रचना के लिए एल्गोरिदम

1) पत्र के साथ संपर्क के बिंदु के एब्सिसा को नामित करें।
2) 1 (ए) की गणना करें।
3) f "(x) खोजें और f" (a) की गणना करें।
4) प्राप्त संख्याओं को a, f(a), (a) को सूत्र (1) में रखें।

उदाहरण 1बिंदु x = 1 पर फलन के आलेख की स्पर्श रेखा के लिए एक समीकरण लिखिए।
आइए एल्गोरिथ्म का उपयोग करें, इस उदाहरण पर विचार करते हुए

अंजीर पर। 126 एक हाइपरबोला दिखाता है, एक सीधी रेखा y \u003d 2x निर्मित होती है।
चित्र दी गई गणनाओं की पुष्टि करता है: वास्तव में, रेखा y \u003d 2-x बिंदु (1; 1) पर हाइपरबोला को छूती है।

उत्तर:वाई \u003d 2-एक्स।
उदाहरण 2फ़ंक्शन के ग्राफ़ पर एक स्पर्शरेखा बनाएं ताकि यह सीधी रेखा y \u003d 4x - 5 के समानांतर हो।
आइए समस्या के सूत्रीकरण को परिष्कृत करें। "एक स्पर्शरेखा खींचना" की आवश्यकता का आमतौर पर अर्थ है "एक स्पर्शरेखा के लिए एक समीकरण बनाना"। यह तर्कसंगत है, क्योंकि यदि कोई व्यक्ति एक स्पर्शरेखा के लिए एक समीकरण की रचना करने में सक्षम था, तो उसके समीकरण के अनुसार निर्देशांक तल पर एक सीधी रेखा के निर्माण में कठिनाइयों का अनुभव होने की संभावना नहीं है।
आइए स्पर्शरेखा समीकरण को संकलित करने के लिए एल्गोरिथ्म का उपयोग करें, यह देखते हुए कि इस उदाहरण में, लेकिन, पिछले उदाहरण के विपरीत, यहां अस्पष्टता है: स्पर्शरेखा बिंदु का भुज स्पष्ट रूप से इंगित नहीं किया गया है।
चलिए इस तरह बात करना शुरू करते हैं। वांछित स्पर्शरेखा सीधी रेखा y \u003d 4x-5 के समानांतर होनी चाहिए। दो रेखाएँ समानांतर होती हैं यदि और केवल यदि उनके ढलान समान हों। इसका मतलब है कि स्पर्शरेखा का ढलान दी गई सीधी रेखा के ढलान के बराबर होना चाहिए: इस प्रकार, हम समीकरण f "(a) \u003d 4 से a का मान ज्ञात कर सकते हैं।
हमारे पास है:
समीकरण से तो, दो स्पर्शरेखाएँ हैं जो समस्या की शर्तों को संतुष्ट करती हैं: एक बिंदु पर 2 के भुज के साथ, दूसरा बिंदु पर -2 के भुज के साथ।
अब आप एल्गोरिथम के अनुसार कार्य कर सकते हैं।

उदाहरण 3बिंदु (0; 1) से फलन के आलेख पर एक स्पर्श रेखा खींचिए
आइए इस उदाहरण पर विचार करते हुए स्पर्शरेखा समीकरण को संकलित करने के लिए एल्गोरिदम का उपयोग करें ध्यान दें कि यहां, उदाहरण 2 में, स्पर्शरेखा बिंदु का भुज स्पष्ट रूप से इंगित नहीं किया गया है। फिर भी, हम एल्गोरिथम के अनुसार कार्य करते हैं।

शर्त के अनुसार, स्पर्शरेखा बिंदु (0; 1) से होकर गुजरती है। समीकरण (2) में x = 0, y = 1 के मान रखने पर, हम प्राप्त करते हैं:
जैसा कि आप देख सकते हैं, इस उदाहरण में, केवल एल्गोरिथम के चौथे चरण में हम स्पर्श बिंदु के एब्सिस्सा को खोजने में कामयाब रहे। मान a \u003d 4 को समीकरण (2) में प्रतिस्थापित करने पर, हम प्राप्त करते हैं:

अंजीर पर। 127 माना उदाहरण का एक ज्यामितीय चित्रण दिखाता है: फ़ंक्शन का एक ग्राफ

32 में, हमने देखा कि एक फलन y = f(x) के लिए, जिसका एक निश्चित बिंदु x पर अवकलज है, सन्निकट समानता रखती है:

आगे के तर्क की सुविधा के लिए, हम संकेतन बदलते हैं: x के बजाय हम a लिखेंगे, इसके बजाय x लिखेंगे, और तदनुसार हम x-a लिखेंगे। तब ऊपर लिखी गई अनुमानित समानता का रूप लेगी:

अब अंजीर पर एक नज़र डालें। 128. बिंदु M (a; f (a)) पर फ़ंक्शन y \u003d f (x) के ग्राफ पर एक स्पर्शरेखा खींची जाती है। x-अक्ष पर a के निकट बिंदु x अंकित करें। यह स्पष्ट है कि f(x) निर्दिष्ट बिंदु x पर फ़ंक्शन के ग्राफ़ की कोटि है। और f (a) + f "(a) (x-a) क्या है? यह उसी बिंदु x के संगत स्पर्शरेखा की कोटि है - सूत्र देखें (1)। सन्निकट समानता (3) का क्या अर्थ है? फ़ंक्शन के अनुमानित मान की गणना करें, स्पर्शरेखा कोटि का मान लिया जाता है।

उदाहरण 4संख्यात्मक व्यंजक 1.02 7 का अनुमानित मान ज्ञात कीजिए।
हम बिंदु x \u003d 1.02 पर फ़ंक्शन y \u003d x 7 का मान ज्ञात करने के बारे में बात कर रहे हैं। हम सूत्र (3) का उपयोग करते हैं, इस बात को ध्यान में रखते हुए कि इस उदाहरण में
परिणामस्वरूप, हमें मिलता है:

यदि हम कैलकुलेटर का उपयोग करते हैं, तो हमें मिलता है: 1.02 7 = 1.148685667...
जैसा कि आप देख सकते हैं, सन्निकटन सटीकता काफी स्वीकार्य है।
उत्तर: 1,02 7 =1,14.

ए.जी. मोर्दकोविच बीजगणित ग्रेड 10

गणित में कैलेंडर-विषयक योजना, वीडियोगणित में ऑनलाइन, स्कूल में गणित डाउनलोड

स्पर्शरेखा एक सीधी रेखा है , जो एक बिंदु पर फ़ंक्शन के ग्राफ़ को स्पर्श करता है और सभी बिंदु फ़ंक्शन के ग्राफ़ से सबसे छोटी दूरी पर होते हैं। इसलिए, स्पर्शरेखा एक निश्चित कोण पर फ़ंक्शन ग्राफ़ पर स्पर्शरेखा से गुजरती है और कई स्पर्शरेखा विभिन्न कोणों पर स्पर्शरेखा बिंदु से नहीं गुजर सकती हैं। स्पर्शरेखा समीकरण और फ़ंक्शन के सामान्य के समीकरणों को व्युत्पन्न का उपयोग करके संकलित किया जाता है।

स्पर्शरेखा समीकरण सरल रेखा समीकरण से लिया गया है .

हम स्पर्शरेखा के समीकरण को प्राप्त करते हैं, और फिर फ़ंक्शन के ग्राफ़ के लिए सामान्य के समीकरण को प्राप्त करते हैं।

आप = केएक्स + बी .

उसमें क- कोणीय गुणांक।

यहां से हमें निम्नलिखित प्रविष्टि मिलती है:

आप - आप 0 = क(एक्स - एक्स 0 ) .

व्युत्पन्न मूल्य एफ "(एक्स 0 ) कार्यों आप = एफ(एक्स) बिंदु पर एक्स0 ढलान के बराबर क= टीजी φ एक बिंदु के माध्यम से खींचे गए फ़ंक्शन के ग्राफ़ के स्पर्शरेखा एम0 (एक्स 0 , आप 0 ) , कहाँ पे आप0 = एफ(एक्स 0 ) . यह क्या है व्युत्पन्न का ज्यामितीय अर्थ .

इस प्रकार, हम प्रतिस्थापित कर सकते हैं कपर एफ "(एक्स 0 ) और निम्नलिखित प्राप्त करें फ़ंक्शन के ग्राफ़ के स्पर्शरेखा का समीकरण :

आप - आप 0 = एफ "(एक्स 0 )(एक्स - एक्स 0 ) .

किसी फ़ंक्शन के ग्राफ़ में स्पर्शरेखा के समीकरण को संकलित करने के कार्यों में (और हम जल्द ही उन पर आगे बढ़ेंगे), उपरोक्त सूत्र से प्राप्त समीकरण को लाने की आवश्यकता है एक सीधी रेखा का सामान्य समीकरण. ऐसा करने के लिए, आपको सभी अक्षरों और संख्याओं को समीकरण के बाईं ओर स्थानांतरित करना होगा, और शून्य को दाईं ओर छोड़ना होगा।

अब सामान्य समीकरण के बारे में। साधारण स्पर्शरेखा के लंबवत फ़ंक्शन के ग्राफ़ पर स्पर्शरेखा बिंदु से गुजरने वाली एक सीधी रेखा है। सामान्य समीकरण :

(एक्स - एक्स 0 ) + एफ "(एक्स 0 )(आप - आप 0 ) = 0

पहले उदाहरण को गर्म करने के लिए, आपको इसे स्वयं हल करने के लिए कहा जाता है, और फिर समाधान को देखें। यह आशा करने का हर कारण है कि यह कार्य हमारे पाठकों के लिए "ठंडा स्नान" नहीं होगा।

उदाहरण 0.एक बिंदु पर फ़ंक्शन के ग्राफ के लिए स्पर्शरेखा के समीकरण और सामान्य के समीकरण की रचना करें एम (1, 1) .

उदाहरण 1फ़ंक्शन के ग्राफ़ के लिए स्पर्शरेखा के समीकरण और सामान्य के समीकरण की रचना करें यदि स्पर्श बिंदु का भुज है।

आइए फ़ंक्शन का व्युत्पन्न खोजें:

अब हमारे पास वह सब कुछ है जिसे स्पर्शरेखा समीकरण प्राप्त करने के लिए सैद्धांतिक संदर्भ में दी गई प्रविष्टि में प्रतिस्थापित करने की आवश्यकता है। हम पाते हैं

इस उदाहरण में, हम भाग्यशाली थे: ढलान शून्य के बराबर निकला, इसलिए समीकरण को सामान्य रूप में लाने के लिए अलग से कोई आवश्यकता नहीं थी। अब हम सामान्य समीकरण लिख सकते हैं:

नीचे दी गई तस्वीर में: बरगंडी में एक समारोह का एक ग्राफ, हरे रंग में एक स्पर्शरेखा, नारंगी में एक सामान्य।

अगला उदाहरण भी जटिल नहीं है: फ़ंक्शन, पिछले एक की तरह, भी एक बहुपद है, लेकिन ढलान गुणांक शून्य के बराबर नहीं होगा, इसलिए एक और चरण जोड़ा जाएगा - समीकरण को सामान्य रूप में लाना।

उदाहरण 2

समाधान। आइए स्पर्श बिंदु की कोटि ज्ञात करें:

आइए फ़ंक्शन का व्युत्पन्न खोजें:

.

आइए संपर्क के बिंदु पर व्युत्पन्न का मान ज्ञात करें, अर्थात स्पर्शरेखा का ढलान:

हम "रिक्त सूत्र" में प्राप्त सभी डेटा को प्रतिस्थापित करते हैं और स्पर्शरेखा समीकरण प्राप्त करते हैं:

हम समीकरण को एक सामान्य रूप में लाते हैं (हम बाईं ओर शून्य के अलावा सभी अक्षरों और संख्याओं को एकत्र करते हैं, और दाईं ओर शून्य छोड़ देते हैं):

हम सामान्य के समीकरण की रचना करते हैं:

उदाहरण 3स्पर्शरेखा के समीकरण की रचना करें और फ़ंक्शन के ग्राफ़ के लिए सामान्य का समीकरण यदि संपर्क बिंदु का भुज है।

समाधान। आइए स्पर्श बिंदु की कोटि ज्ञात करें:

आइए फ़ंक्शन का व्युत्पन्न खोजें:

.

आइए संपर्क के बिंदु पर व्युत्पन्न का मान ज्ञात करें, अर्थात स्पर्शरेखा का ढलान:

.

हम स्पर्शरेखा का समीकरण पाते हैं:

समीकरण को एक सामान्य रूप में लाने से पहले, आपको इसे थोड़ा "गठबंधन" करने की आवश्यकता है: शब्द को 4 से गुणा करें। हम ऐसा करते हैं और समीकरण को एक सामान्य रूप में लाते हैं:

हम सामान्य के समीकरण की रचना करते हैं:

उदाहरण 4स्पर्शरेखा के समीकरण की रचना करें और फ़ंक्शन के ग्राफ़ के लिए सामान्य का समीकरण यदि संपर्क बिंदु का भुज है।

समाधान। आइए स्पर्श बिंदु की कोटि ज्ञात करें:

.

आइए फ़ंक्शन का व्युत्पन्न खोजें:

आइए संपर्क के बिंदु पर व्युत्पन्न का मान ज्ञात करें, अर्थात स्पर्शरेखा का ढलान:

.

हमें स्पर्शरेखा समीकरण मिलता है:

हम समीकरण को एक सामान्य रूप में लाते हैं:

हम सामान्य के समीकरण की रचना करते हैं:

स्पर्शरेखा और सामान्य समीकरण लिखते समय एक सामान्य गलती यह नोटिस नहीं करना है कि उदाहरण में दिया गया फ़ंक्शन जटिल है और एक साधारण फ़ंक्शन के व्युत्पन्न के रूप में इसके व्युत्पन्न की गणना करें। निम्नलिखित उदाहरण पहले से ही हैं जटिल कार्य(संबंधित पाठ एक नई विंडो में खुलेगा)।

उदाहरण 5स्पर्शरेखा के समीकरण की रचना करें और फ़ंक्शन के ग्राफ़ के लिए सामान्य का समीकरण यदि संपर्क बिंदु का भुज है।

समाधान। आइए स्पर्श बिंदु की कोटि ज्ञात करें:

ध्यान! स्पर्शरेखा के तर्क के बाद से यह कार्य जटिल है (2 एक्स) स्वयं एक फ़ंक्शन है। इसलिए, हम एक फ़ंक्शन के व्युत्पन्न को एक जटिल फ़ंक्शन के व्युत्पन्न के रूप में पाते हैं।

आलेख परिभाषाओं का विस्तृत विवरण देता है, ग्राफिक संकेतन के साथ व्युत्पन्न का ज्यामितीय अर्थ। स्पर्शरेखा रेखा के समीकरण को उदाहरण सहित माना जाएगा, द्वितीय कोटि की स्पर्श रेखा से वक्रों के समीकरण मिलेंगे।

यांडेक्स.आरटीबी आर-ए-339285-1 परिभाषा 1

सीधी रेखा y \u003d k x + b के झुकाव के कोण को कोण α कहा जाता है, जिसे x-अक्ष की सकारात्मक दिशा से सीधी रेखा y \u003d k x + b तक सकारात्मक दिशा में मापा जाता है।

आकृति में, दिशा बैल को एक हरे तीर और एक हरे रंग के चाप और लाल चाप द्वारा झुकाव के कोण द्वारा दर्शाया गया है। नीली रेखा एक सीधी रेखा को दर्शाती है।

परिभाषा 2

सीधी रेखा y \u003d k x + b की ढलान को संख्यात्मक गुणांक k कहा जाता है।

ढलान सीधी रेखा के ढलान के बराबर है, दूसरे शब्दों में k = t g α ।

• सीधी रेखा का ढलान 0 तभी होता है जब o x समानांतर होता है और ढलान शून्य के बराबर होता है, क्योंकि शून्य की स्पर्शरेखा 0 होती है। अत: समीकरण का रूप y = b होगा।
• यदि सीधी रेखा y = k x + b का झुकाव कोण नुकीला हो, तो स्थितियाँ 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 , और ग्राफ में वृद्धि हुई है।
• यदि α \u003d π 2, तो रेखा का स्थान x के लंबवत है। समानता x = c द्वारा निर्दिष्ट की जाती है, जिसका मान c एक वास्तविक संख्या है।
• यदि सीधी रेखा y = k x + b का झुकाव कोण अधिक है, तो यह शर्तों π 2 के अनुरूप है< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

एक छेदक एक सीधी रेखा है जो फलन f (x) के 2 बिंदुओं से होकर गुजरती है। दूसरे शब्दों में, एक छेदक एक सीधी रेखा है जो किसी दिए गए फ़ंक्शन के ग्राफ़ पर किन्हीं दो बिंदुओं से होकर गुजरती है।

चित्र से पता चलता है कि ए बी एक छेदक है, और एफ (एक्स) एक काला वक्र है, α एक लाल चाप है, जो छेदक के झुकाव के कोण को दर्शाता है।

जब एक सीधी रेखा का ढलान झुकाव के कोण के स्पर्शरेखा के बराबर होता है, तो यह स्पष्ट होता है कि एक समकोण त्रिभुज A B C की स्पर्शरेखा आसन्न पैर के विपरीत पैर के संबंध में पाई जा सकती है।

परिभाषा 4

हमें फॉर्म का सेकेंट खोजने का सूत्र मिलता है:

k = tg α = BCAC = f (x B) - fx A x B - x A , जहां बिंदुओं A और B के भुज x A , x B , और f (x A), f (x) के मान हैं बी) इन बिंदुओं पर मूल्य कार्य हैं।

जाहिर है, सेकेंड का ढलान समानता k \u003d f (x B) - f (x A) x B - x A या k \u003d f (x A) - f (x B) x A - x का उपयोग करके परिभाषित किया गया है। बी, और समीकरण को y = f (x B) - f (x A) x B - x A x - x A + f (x A) के रूप में लिखा जाना चाहिए या
वाई = एफ (एक्स ए) - एफ (एक्स बी) एक्स ए - एक्स बी एक्स - एक्स बी + एफ (एक्स बी)।

सेकेंट नेत्रहीन रूप से ग्राफ़ को 3 भागों में विभाजित करता है: बिंदु A के बाईं ओर, A से B तक, B के दाईं ओर। नीचे दिए गए आंकड़े से पता चलता है कि तीन सेकेंट हैं जिन्हें समान माना जाता है, अर्थात वे हैं एक समान समीकरण का उपयोग करके सेट करें।

परिभाषा के अनुसार, यह स्पष्ट है कि इस मामले में रेखा और उसका छेदक मेल खाता है।

एक छेदक किसी दिए गए फ़ंक्शन के ग्राफ़ को कई बार प्रतिच्छेद कर सकता है। यदि सेकेंड के लिए फॉर्म y \u003d 0 का समीकरण है, तो साइनसॉइड के साथ चौराहे के बिंदुओं की संख्या अनंत है।

परिभाषा 5

फ़ंक्शन f (x) के बिंदु x 0 पर स्पर्शरेखा; f (x 0) दिए गए बिंदु x 0 से गुजरने वाली एक सीधी रेखा कहलाती है; f (x 0) , एक खंड की उपस्थिति के साथ जिसमें x 0 के करीब कई x मान हैं।

उदाहरण 1

आइए नीचे दिए गए उदाहरण पर करीब से नज़र डालें। तब यह देखा जा सकता है कि फ़ंक्शन y = x + 1 द्वारा दी गई रेखा को निर्देशांक (1 ; 2) वाले बिंदु पर y = 2 x की स्पर्शरेखा माना जाता है। स्पष्टता के लिए, (1; 2) के करीब मान वाले ग्राफ़ पर विचार करना आवश्यक है। फ़ंक्शन y = 2 x को काले रंग में चिह्नित किया गया है, नीली रेखा स्पर्शरेखा है, लाल बिंदु प्रतिच्छेदन बिंदु है।

जाहिर है, y \u003d 2 x लाइन y \u003d x + 1 के साथ विलीन हो जाता है।

स्पर्शरेखा का निर्धारण करने के लिए, किसी को स्पर्शरेखा A B के व्यवहार पर विचार करना चाहिए क्योंकि बिंदु B, बिंदु A तक अनंत रूप से पहुंचता है। स्पष्टता के लिए, हम एक आकृति प्रस्तुत करते हैं।

नीली रेखा द्वारा इंगित छेदक ए बी, स्पर्शरेखा की स्थिति में ही जाता है, और छेदक α के झुकाव का कोण स्पर्शरेखा α x के झुकाव के कोण के लिए शुरू हो जाएगा।

परिभाषा 6

बिंदु A पर फ़ंक्शन y \u003d f (x) के ग्राफ़ की स्पर्शरेखा, बिंदु A B की बिंदु A की ओर झुकाव की सीमित स्थिति है, अर्थात B → A।

अब हम एक बिंदु पर किसी फलन के अवकलज के ज्यामितीय अर्थ पर विचार करते हैं।

आइए फ़ंक्शन f (x) के लिए secant AB पर विचार करें, जहां A और B निर्देशांक x 0, f (x 0) और x 0 + ∆ x, f (x 0 + ∆ x), और के साथ हैं। x को तर्क की वृद्धि के रूप में दर्शाया गया है। अब फलन y = ∆ f (x) = f (x 0 + x) - f (∆ x) का रूप लेगा। स्पष्टता के लिए, आइए एक उदाहरण के रूप में एक तस्वीर लें।

परिणामी समकोण त्रिभुज A B C पर विचार करें। हम हल के लिए स्पर्शरेखा की परिभाषा का उपयोग करते हैं, अर्थात, हम अनुपात ∆ y ∆ x = t g α प्राप्त करते हैं। स्पर्शरेखा की परिभाषा से यह पता चलता है कि lim ∆ x → 0 ∆ y ∆ x = t g α x । एक बिंदु पर व्युत्पन्न नियम के अनुसार, हमारे पास बिंदु x 0 पर व्युत्पन्न f (x) को तर्क की वृद्धि के लिए फ़ंक्शन की वृद्धि के अनुपात की सीमा कहा जाता है, जहां x → 0, फिर f (x 0) = lim x → 0 ∆ y ∆ x के रूप में निरूपित किया जाता है।

यह इस प्रकार है कि f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, जहां k x को स्पर्शरेखा के ढलान के रूप में दर्शाया जाता है।

अर्थात्, हम पाते हैं कि f' (x) बिंदु x 0 पर मौजूद हो सकता है और, x 0 के बराबर संपर्क बिंदु पर फ़ंक्शन के दिए गए ग्राफ़ की स्पर्शरेखा की तरह, f 0 (x 0), जहां मान बिंदु पर स्पर्शरेखा का ढलान बिंदु x 0 पर व्युत्पन्न के बराबर है। तब हम पाते हैं कि k x = f "(x 0) ।

एक बिंदु पर एक फ़ंक्शन के व्युत्पन्न का ज्यामितीय अर्थ यह है कि एक ही बिंदु पर ग्राफ के स्पर्शरेखा के अस्तित्व की अवधारणा दी गई है।

समतल में किसी भी सीधी रेखा का समीकरण लिखने के लिए उस बिंदु के साथ ढलान होना आवश्यक है जिससे वह गुजरता है। चौराहे पर इसका पदनाम x 0 के रूप में लिया जाता है।

फ़ंक्शन y \u003d f (x) के बिंदु x 0 पर स्पर्शरेखा का समीकरण, f 0 (x 0) रूप लेता है y \u003d f "(x 0) x - x 0 + f (x) 0)।

इसका अर्थ यह है कि व्युत्पन्न f "(x 0) का अंतिम मान स्पर्शरेखा की स्थिति का निर्धारण कर सकता है, अर्थात लिम x → x 0 + 0 f" (x) = और lim x → x 0 की स्थिति के तहत लंबवत रूप से - 0 f "(x ) = या lim x → x 0 + 0 f "(x) lim x → x 0 - 0 f "(x) की स्थिति में बिल्कुल भी अनुपस्थिति।

स्पर्शरेखा का स्थान उसके ढलान kx \u003d f "(x 0) के मान पर निर्भर करता है। x अक्ष के समानांतर होने पर, हमें वह kk \u003d 0 मिलता है, जब लगभग y - kx \u003d के समानांतर, और स्पर्शरेखा समीकरण का रूप x \u003d x 0 kx > 0 के साथ बढ़ता है, kx . के रूप में घटता है< 0 .

उदाहरण 2

फ़ंक्शन के ग्राफ़ के लिए स्पर्शरेखा के समीकरण को संकलित करें y \u003d पूर्व + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 के कोण की परिभाषा के साथ निर्देशांक (1; 3) के साथ एक बिंदु पर झुकाव।

समाधान

धारणा से, हमारे पास यह है कि फ़ंक्शन सभी वास्तविक संख्याओं के लिए परिभाषित किया गया है। हम पाते हैं कि स्थिति (1 ; 3) द्वारा निर्दिष्ट निर्देशांक वाला बिंदु संपर्क बिंदु है, फिर x 0 = - 1, f (x 0) = - 3।

1 के मान वाले बिंदु पर अवकलज ज्ञात करना आवश्यक है। हमें वह मिलता है

y "= पूर्व + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" == पूर्व + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = पूर्व + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

संपर्क बिंदु पर f' (x) का मान स्पर्शरेखा का ढाल होता है, जो ढाल की स्पर्श रेखा के बराबर होता है।

तब k x = t g α x = y "(x 0) = 3 3

यह इस प्रकार है कि α x = a r c t g 3 3 = π 6

उत्तर:स्पर्शरेखा समीकरण रूप लेता है

y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3

स्पष्टता के लिए, हम एक ग्राफिक चित्रण में एक उदाहरण देते हैं।

मूल फ़ंक्शन ग्राफ़ के लिए काले रंग का उपयोग किया जाता है, नीला रंग स्पर्शरेखा छवि है, लाल बिंदु स्पर्श बिंदु है। दाईं ओर की आकृति एक बढ़े हुए दृश्य को दर्शाती है।

उदाहरण 3

किसी दिए गए फ़ंक्शन के ग्राफ़ पर स्पर्शरेखा के अस्तित्व का पता लगाएं
y = 3 x - 1 5 + 1 निर्देशांक के साथ बिंदु पर (1 ; 1)। एक समीकरण लिखिए और झुकाव का कोण ज्ञात कीजिए।

समाधान

धारणा से, हमारे पास यह है कि दिए गए फ़ंक्शन का डोमेन सभी वास्तविक संख्याओं का समूह है।

आइए व्युत्पन्न खोजने के लिए आगे बढ़ें

y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

यदि x 0 = 1 है, तो f' (x) परिभाषित नहीं है, लेकिन सीमाएँ lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 के रूप में लिखी जाती हैं। 5 1 + 0 = + और लिम x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + , जिसका अर्थ है अस्तित्व पर लंबवत स्पर्शरेखा बिंदु (1; 1)।

उत्तर:समीकरण x \u003d 1 का रूप लेगा, जहां झुकाव का कोण 2 के बराबर होगा।

आइए इसे स्पष्टता के लिए ग्राफ़ करें।

उदाहरण 4

फलन ग्राफ y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 के बिंदु ज्ञात कीजिए, जहाँ

1. स्पर्शरेखा मौजूद नहीं है;
2. स्पर्शरेखा x के समानांतर है;
3. स्पर्शरेखा रेखा y = 8 5 x + 4 के समानांतर है।

समाधान

परिभाषा के क्षेत्र पर ध्यान देना आवश्यक है। धारणा से, हमारे पास यह है कि फ़ंक्शन सभी वास्तविक संख्याओं के सेट पर परिभाषित होता है। मॉड्यूल का विस्तार करें और सिस्टम को अंतराल x - के साथ हल करें; 2 और [- 2 ; +∞) । हमें वह मिलता है

वाई = - 1 15 x 3 + 18 x 2 + 105 x + 176, x - ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x [ - 2 ; +∞)

फ़ंक्शन को अलग करने की आवश्यकता है। हमारे पास वह है

y "= - 1 15 x 3 + 18 x 2 + 105 x + 176", x - ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x [- 2; + ∞) y" = - 1 5 (x 2 + 12 x + 35), x - ; - 2 1 5 x 2 - 4 x + 3 , x [ - 2 ; +∞)

जब x = - 2, तब अवकलज मौजूद नहीं होता क्योंकि उस बिंदु पर एकतरफा सीमाएँ समान नहीं होती हैं:

लिम एक्स → - 2 - 0 वाई "(एक्स) = लिम एक्स → - 2 - 0 - 1 5 (एक्स 2 + 12 एक्स + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 लिम x → - 2 + 0 y "(x) = लिम x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

हम बिंदु x \u003d - 2 पर फ़ंक्शन के मान की गणना करते हैं, जहां हमें वह मिलता है

1. y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, यानी स्पर्शरेखा पर बिंदु (- 2; - 2) मौजूद नहीं होगा।
2. ढलान शून्य होने पर स्पर्शरेखा x के समानांतर होती है। फिर kx \u003d tg α x \u003d f "(x 0)। यानी, ऐसे x के मानों को खोजना आवश्यक है जब फ़ंक्शन का व्युत्पन्न इसे शून्य में बदल देता है। अर्थात्, मान \u200b\u200bf '(x) और स्पर्श बिंदु होंगे, जहां स्पर्शरेखा x के समानांतर होती है।

जब एक्स - ; - 2, फिर - 1 5 (x 2 + 12 x + 35) = 0, और x (- 2 ; + ∞) के लिए हमें 1 5 (x 2 - 4 x + 3) = 0 प्राप्त होता है।

1 5 (x 2 + 12 x + 35) = 0 डी = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 - ; - 2 x 2 = - 12 - 4 2 = - 7 - ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2; + x 4 = 4 + 4 2 = 3 - 2; +∞

हम फ़ंक्शन के संबंधित मानों की गणना करते हैं

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

इसलिए - 5; 8 5 , - 4 ; 4 3 , 1 ; 85, 3; 4 3 फलन के ग्राफ के वांछित बिन्दु माने जाते हैं।

समाधान के चित्रमय प्रतिनिधित्व पर विचार करें।

काली रेखा फ़ंक्शन का ग्राफ़ है, लाल बिंदु स्पर्श बिंदु हैं।

1. जब रेखाएँ समानांतर होती हैं, तो ढलान समान होते हैं। फिर फ़ंक्शन के ग्राफ़ के बिंदुओं की खोज करना आवश्यक है, जहां ढलान मान 8 5 के बराबर होगा। ऐसा करने के लिए, आपको y "(x) = 8 5. फॉर्म के समीकरण को हल करने की आवश्यकता है। फिर, यदि x - ; - 2, तो हमें वह मिलता है - 1 5 (x 2 + 12 x + 35) = 8 5, और यदि x ( - 2 ; + ∞) , तो 1 5 (x 2 - 4 x + 3) = 8 5 ।

पहले समीकरण का कोई मूल नहीं है क्योंकि विवेचक शून्य से कम है। आइए इसे लिख लें

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 डी = 12 2 - 4 43 = - 28< 0

एक अन्य समीकरण के दो वास्तविक मूल हैं, तब

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 - 2; + x 2 = 4 + 36 2 = 5 - 2; +∞

आइए फ़ंक्शन के मूल्यों को खोजने के लिए आगे बढ़ें। हमें वह मिलता है

वाई 1 = वाई (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 वाई 2 = वाई (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

मान के साथ अंक - 1 ; 4 15 , 5 ; 8 3 ऐसे बिंदु हैं जहां स्पर्शरेखा रेखा y = 8 5 x + 4 के समानांतर हैं।

उत्तर:काली रेखा - फ़ंक्शन का ग्राफ, लाल रेखा - ग्राफ़ y \u003d 8 5 x + 4, नीली रेखा - बिंदुओं पर स्पर्शरेखा - 1; 4 15 , 5 ; 8 3।

दिए गए फलनों के लिए अनंत संख्या में स्पर्श रेखाओं का अस्तित्व संभव है।

उदाहरण 5

फलन y = 3 cos 3 2 x - π 4 - 1 3 की सभी उपलब्ध स्पर्श रेखाओं के समीकरण लिखिए, जो रेखा y = - 2 x + 1 2 के लंबवत हैं।

समाधान

स्पर्शरेखा समीकरण को संकलित करने के लिए, रेखाओं की लंबवतता की स्थिति के आधार पर, स्पर्शरेखा बिंदु के गुणांक और निर्देशांक ज्ञात करना आवश्यक है। परिभाषा इस तरह लगती है: सीधी रेखाओं के लंबवत ढलानों का गुणनफल -1 के बराबर होता है, अर्थात इसे k x · k = - 1 के रूप में लिखा जाता है। इस शर्त से कि ढलान सीधी रेखा के लंबवत है और k = - 2 के बराबर है, तो k x = - 1 k = - 1 - 2 = 1 2।

अब हमें स्पर्श बिंदुओं के निर्देशांक खोजने की आवश्यकता है। आपको x खोजने की आवश्यकता है, जिसके बाद किसी दिए गए फ़ंक्शन के लिए इसका मान है। ध्यान दें कि बिंदु पर व्युत्पन्न के ज्यामितीय अर्थ से
x 0 हमें वह k x \u003d y "(x 0) मिलता है। इस समानता से, हम स्पर्श बिंदुओं के लिए x मान पाते हैं।

हमें वह मिलता है

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - पाप 3 2 x 0 - 4 3 2 x 0 - 4 "= - 3 पाप 3 2 x 0 - 4 3 2 \u003d - 9 2 पाप 3 2 x 0 - 4 kx \u003d y "(x 0) - 9 2 पाप 3 2 x 0 - 4 \u003d 1 2 पाप 3 2 x 0 - 4 = - 1 9

इस त्रिकोणमितीय समीकरण का उपयोग स्पर्श बिंदुओं के निर्देशांक की गणना के लिए किया जाएगा।

3 2 x 0 - 4 = a r c sin - 1 9 + 2 k या 3 2 x 0 - 4 = - a r c sin - 1 9 + 2 k

3 2 x 0 - 4 = - a r c sin 1 9 + 2 k या 3 2 x 0 - 4 = + a r c sin 1 9 + 2 k

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 k या x 0 = 2 3 5 4 + a r c sin 1 9 + 2 k, k Z

Z पूर्णांकों का समुच्चय है।

संपर्क के x बिंदु मिले। अब आपको y मानों की खोज में जाना होगा:

y 0 = 3 cos 3 2 x 0 - 4 - 1 3

y 0 = 3 1 - पाप 2 3 2 x 0 - 4 - 1 3 या y 0 = 3 - 1 - पाप 2 3 2 x 0 - 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 या y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 या y 0 = - 4 5 + 1 3

यहाँ से हम पाते हैं कि 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 4 + a r c sin 1 9 + 2 k ; - 4 5 + 1 3 स्पर्श बिंदु हैं।

उत्तर:आवश्यक समीकरण के रूप में लिखा जाएगा

y = 1 2 x - 2 3 π 4 - चाप पाप 1 9 + 2 k + 4 5 - 1 3, y = 1 2 x - 2 3 5 π 4 + चाप पाप 1 9 + 2 k - 4 5 + 1 3 , कश्मीर ज़ू

एक दृश्य प्रतिनिधित्व के लिए, समन्वय रेखा पर फ़ंक्शन और स्पर्शरेखा पर विचार करें।

चित्र से पता चलता है कि फ़ंक्शन का स्थान अंतराल पर है [ - 10 ; 10 ] , जहां काली रेखा फलन का आलेख है, नीली रेखाएं y = - 2 x + 1 2 के रूप की दी गई रेखा के लंबवत स्पर्श रेखाएं हैं। लाल बिंदु स्पर्श बिंदु हैं।

दूसरे क्रम के वक्रों के विहित समीकरण एकल-मूल्यवान फलन नहीं हैं। उनके लिए स्पर्शरेखा समीकरण प्रसिद्ध योजनाओं के अनुसार संकलित किए जाते हैं।

वृत्त की स्पर्श रेखा

एक बिंदु x c e n t e r पर केंद्रित एक वृत्त सेट करना; y c e n t e r और त्रिज्या R, सूत्र x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 का उपयोग किया जाता है।

इस समानता को दो कार्यों के मिलन के रूप में लिखा जा सकता है:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

पहला फ़ंक्शन सबसे ऊपर और दूसरा सबसे नीचे है, जैसा कि चित्र में दिखाया गया है।

किसी बिंदु x 0 पर वृत्त का समीकरण बनाना; y 0 , जो ऊपरी या निचले अर्धवृत्त में स्थित है, आपको y \u003d R 2 - x - xcenter 2 + ycenter या y \u003d - R 2 - x - xcenter 2 + के रूप के फ़ंक्शन ग्राफ़ का समीकरण खोजना चाहिए। निर्दिष्ट बिंदु पर ycenter।

जब बिंदुओं पर x c e n t e r ; वाई सी ई एन टी ई आर + आर और एक्स सी ई एन टी ई आर; y c e n t e r - R स्पर्शरेखा समीकरण y = y c e n t e r + R और y = y c e n t e r - R और बिंदुओं x c e n t e r + R द्वारा दी जा सकती हैं; वाई सी ई एन टी ई आर और
एक्स सी ई एन टी ई आर - आर; y c e n t e r, y के समांतर होगा, तो हमें x = x c e n t e r + R और x = x c e n t e r - R के रूप के समीकरण प्राप्त होंगे।

दीर्घवृत्त की स्पर्शरेखा

जब दीर्घवृत्त x c e n t e r पर केंद्रित होता है; y c e n t e r अर्धअक्ष a और b के साथ, तो इसे समीकरण x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 का उपयोग करके दिया जा सकता है।

एक दीर्घवृत्त और एक वृत्त को दो कार्यों, अर्थात् ऊपरी और निचले अर्ध-दीर्घवृत्त के संयोजन से निरूपित किया जा सकता है। तब हमें वह मिलता है

y = b a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a 2 - (x - x c e n t e r) 2 + y c e n t e r

यदि स्पर्शरेखाएँ दीर्घवृत्त के शीर्षों पर स्थित हों, तो वे x या लगभग y के समांतर होती हैं। स्पष्टता के लिए, नीचे दिए गए चित्र पर विचार करें।

उदाहरण 6

दीर्घवृत्त x - 3 2 4 + y - 5 2 25 = 1 की स्पर्शरेखा का समीकरण x = 2 के बराबर x मान वाले बिंदुओं पर लिखें।

समाधान

x = 2 के मान के अनुरूप स्पर्श बिंदुओं को खोजना आवश्यक है। हम दीर्घवृत्त के मौजूदा समीकरण में एक प्रतिस्थापन करते हैं और वह प्राप्त करते हैं

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

फिर 2 ; 5 3 2 + 5 और 2; - 5 3 2 + 5 स्पर्शरेखा बिंदु हैं जो ऊपरी और निचले अर्ध-दीर्घवृत्त से संबंधित हैं।

आइए y के संबंध में एक दीर्घवृत्त के समीकरण को खोजने और हल करने के लिए आगे बढ़ते हैं। हमें वह मिलता है

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

यह स्पष्ट है कि ऊपरी अर्ध-दीर्घवृत्त को y = 5 + 5 2 4 - x - 3 2 के रूप में निर्दिष्ट किया जाता है, और निचला एक y = 5 - 5 2 4 - x - 3 2 ।

हम एक बिंदु पर किसी फ़ंक्शन के ग्राफ़ पर स्पर्शरेखा के समीकरण को तैयार करने के लिए मानक एल्गोरिदम लागू करते हैं। हम लिखते हैं कि बिंदु 2 पर पहली स्पर्शरेखा के लिए समीकरण; 5 3 2 + 5 इस तरह दिखेगा

वाई "= 5 + 5 2 4 - एक्स - 3 2" = 5 2 1 2 4 - (एक्स - 3) 2 4 - (एक्स - 3) 2 "= - 5 2 एक्स - 3 4 - ( एक्स - 3 ) 2 y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 y = 5 2 3 (x - 2) + 5 3 2 + 5

हम पाते हैं कि बिंदु पर मान के साथ दूसरी स्पर्शरेखा का समीकरण
2; - 5 3 2 + 5 बन जाता है

y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = 5 2 x - 3 4 - (x - 3) 2 y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + वाई 0 वाई = - 5 2 3 (एक्स - 2) - 5 3 2 + 5

आलेखीय रूप से, स्पर्शरेखाओं को निम्न प्रकार से दर्शाया जाता है:

हाइपरबोले की स्पर्शरेखा

जब अतिपरवलय का केंद्र x c e n t e r पर होता है; y c e n t e r और शीर्ष x c e n t e r + α ; वाई सी ई एन टी ई आर और एक्स सी ई एन टी ई आर - α ; y c e n t e r , असमानता x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 दिया जाता है यदि शीर्षों के साथ x c e n t e r ; वाई सी ई एन टी ई आर + बी और एक्स सी ई एन टी ई आर; y c e n t e r - b तब असमानता x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 द्वारा दिया जाता है।

हाइपरबोला को फॉर्म के दो संयुक्त कार्यों के रूप में दर्शाया जा सकता है

y = ba (x - xcenter) 2 - a 2 + ycentery = - ba (x - xcenter) 2 - a 2 + ycenter या y = ba (x - xcenter) 2 + a 2 + ycentery = - ba (x - xcenter) ) 2 + ए 2 + वाईसेंटर

पहले मामले में, हमारे पास स्पर्शरेखा y के समानांतर हैं, और दूसरे में, वे x के समानांतर हैं।

यह इस प्रकार है कि एक हाइपरबोला के स्पर्शरेखा के समीकरण को खोजने के लिए, यह पता लगाना आवश्यक है कि स्पर्शरेखा बिंदु किस कार्य से संबंधित है। इसे निर्धारित करने के लिए, समीकरणों में प्रतिस्थापन करना और पहचान के लिए उनकी जांच करना आवश्यक है।

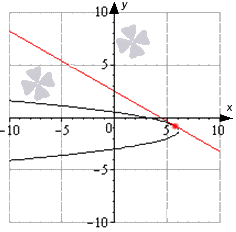
उदाहरण 7

बिंदु 7 पर अतिपरवलय x - 3 2 4 - y + 3 2 9 = 1 की स्पर्श रेखा का समीकरण लिखिए; - 3 3 - 3।

समाधान

2 कार्यों का उपयोग करके हाइपरबोला खोजने के समाधान के रिकॉर्ड को बदलना आवश्यक है। हमें वह मिलता है

x - 3 2 4 - y + 3 2 9 = 1 y + 3 2 9 = x - 3 2 4 - 1 y + 3 2 = 9 x - 3 2 4 - 1 y + 3 = 3 2 x - 3 2 - 4 या y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

यह पता लगाना आवश्यक है कि निर्देशांक 7 के साथ दिया गया बिंदु किस कार्य से संबंधित है; - 3 3 - 3।

जाहिर है, पहले फ़ंक्शन की जांच करने के लिए, यह आवश्यक है y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, तो बिंदु ग्राफ से संबंधित नहीं है, चूंकि समानता संतुष्ट नहीं है।

दूसरे फलन के लिए, हमारे पास y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 है, जिसका अर्थ है कि बिंदु दिए गए ग्राफ से संबंधित है। यहाँ से आपको ढाल गुणांक ज्ञात करना चाहिए।

हमें वह मिलता है

y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ kx = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

उत्तर:स्पर्शरेखा समीकरण के रूप में प्रतिनिधित्व किया जा सकता है

वाई = - 3 एक्स - 7 - 3 3 - 3 = - 3 एक्स + 4 3 - 3

इसकी कल्पना इस प्रकार की जाती है:

परवलय की स्पर्शरेखा

बिंदु x 0, y (x 0) पर परवलय y \u003d ax 2 + bx + c पर स्पर्शरेखा के समीकरण की रचना करने के लिए, आपको मानक एल्गोरिथ्म का उपयोग करना होगा, फिर समीकरण y \u003d y " का रूप लेगा। (x 0) x - x 0 + y ( x 0) शीर्ष पर ऐसी स्पर्श रेखा x के समानांतर होती है।

परवलय x = a y 2 + b y + c को दो कार्यों के मिलन के रूप में परिभाषित किया जाना चाहिए। इसलिए, हमें y के समीकरण को हल करने की आवश्यकता है। हमें वह मिलता है

x = ay 2 + by + c ⇔ ay 2 + by + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 ay = - बी - बी 2 - 4 ए (सी - एक्स) 2 ए

आइए इसे इस प्रकार ग्राफ़ करें:

यह पता लगाने के लिए कि कोई बिंदु x 0 , y (x 0) किसी फ़ंक्शन से संबंधित है या नहीं, मानक एल्गोरिथम का धीरे से पालन करें। ऐसी स्पर्श रेखा परवलय के सन्दर्भ में y के समांतर होगी।

उदाहरण 8

ग्राफ़ x - 2 y 2 - 5 y + 3 की स्पर्शरेखा के लिए समीकरण लिखें जब हमारे पास 150 ° की स्पर्शरेखा ढलान हो।

समाधान

हम परवलय को दो फलनों के रूप में निरूपित करते हुए समाधान की शुरुआत करते हैं। हमें वह मिलता है

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 xy = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 एक्स - 4

ढलान का मान इस फ़ंक्शन के बिंदु x 0 पर व्युत्पन्न के मान के बराबर होता है और ढलान की स्पर्शरेखा के बराबर होता है।

हम पाते हैं:

k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3

यहां से हम स्पर्श बिंदुओं के लिए x का मान निर्धारित करते हैं।

पहला फ़ंक्शन इस प्रकार लिखा जाएगा

y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

जाहिर है, कोई वास्तविक जड़ें नहीं हैं, क्योंकि हमें एक नकारात्मक मूल्य मिला है। हम यह निष्कर्ष निकालते हैं कि ऐसे फलन के लिए 150° के कोण वाली कोई स्पर्श रेखा नहीं है।

दूसरा फ़ंक्शन इस प्रकार लिखा जाएगा

y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

हमारे पास वह स्पर्श बिंदु है - 23 4 ; - 5 + 3 4।

उत्तर:स्पर्शरेखा समीकरण रूप लेता है

वाई = - 1 3 एक्स - 23 4 + - 5 + 3 4

आइए इसे इस तरह से ग्राफ़ करें:

यदि आप टेक्स्ट में कोई गलती देखते हैं, तो कृपया उसे हाइलाइट करें और Ctrl+Enter दबाएं