Свойства функции как определять. Степенная функция, ее свойства и графики

1) Область определения функции и область значений функции .

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена. Область значений функции - это множество всех действительных значений y , которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции .

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции .

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции .

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции .

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x) . График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x ). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции .

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

7) Периодическость функции .

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

19. Основные элементарные функции, их свойства и графики. Применение функ-ций в экономике.

Основные элементарные функции. Их свойства и графики

1. Линейная функция.

Линейной функцией называется функция вида , где х - переменная, а и b - действительные числа.

Число а называют угловым коэффициентом прямой, он равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. Графиком линейной функции является прямая линия. Она определяется двумя точками.

Свойства линейной функции

1. Область определения - множество всех действительных чисел: Д(y)=R

2. Множество значений - множество всех действительных чисел: Е(у)=R

3. Функция принимает нулевое значение при или.

4. Функция возрастает (убывает) на всей области определения.

5. Линейная функция непрерывная на всей области определения, дифференцируемая и .

2. Квадратичная функция.

Функция вида , где х - переменная, коэффициенты а, b, с - действительные числа, называетсяквадратичной.

Нули функции
Нулём функции называется то значение х , при котором функция обращается в 0, то есть f(x)=0.

Нули – это точки пересечения графика функции с осью Ох.

Четность функции
Функция называется чётной, если для любого х из области определения выполняется равенство f(-x) = f(x)

Четная функция симметрична относительно оси Оу

Нечетность функции
Функция называется нечётной, если для любого х из области определения выполняется равенство f(-x) = -f(x).

Нечетная функция симметрична относительно начала координат.
Функция которая не является ни чётной,ни нечётной называется функцией общего вида.

Возрастание функции
Функция f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е.

Убывание функции
Функция f(x) называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е.

Промежутки, на которых функция либо только убывает, либо только возрастает, называются промежутками монотонности . Функция f(x) имеет 3 промежутка монотонности:

Находят промежутки монотонности с помощью сервиса Интервалы возрастания и убывания функции

Локальный максимум
Точка х 0 называется точкой локального максимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0) > f(x)

Локальный минимум
Точка х 0 называется точкой локального минимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0) < f(x).

Точки локального максимума и точки локального минимума называются точками локального экстремума.

точки локального экстремума.

Периодичность функции
Функция f(x) называется периодичной, с периодом Т , если для любого х выполняется равенство f(x+T) = f(x) .

Промежутки знакопостоянства
Промежутки, на которых функция либо только положительна, либо только отрицательна, называются промежутками знакопостоянства.

Непрерывность функции
Функция f(x) называется непрерывной в точке x 0 , если предел функции при x → x 0 равен значению функции в этой точке, т.е. .

Точки разрыва
Точки, в которых нарушено условие непрерывности называются точками разрыва функции.

x 0 - точка разрыва.

Общая схема для построения графиков функций

1. Найти область определения функции D(y).

2. Найти точки пересечения графика функций с осями координат.

3. Исследовать функцию на четность или нечетность.

4. Исследовать функцию на периодичность.

5. Найти промежутки монотонности и точки экстремума функции.

6. Найти промежутки выпуклости и точки перегиба функции.

7. Найти асимптоты функции.

8. По результатам исследования построить график.

Пример: Исследовать функцию и построить ее график: y = x 3 – 3x

1) Функция определена на всей числовой оси, т. е. ее область определения D(y) = (-∞; +∞).

2) Найдем точки пересечения с осями координат:

с осью ОХ: решим уравнение x 3 – 3x = 0

с осью ОY: y(0) = 0 3 – 3*0 = 0

3) Выясним, не является ли функция четной или нечетной:

y(-x) = (-x) 3 – 3(-x) = -x 3 + 3x = - (x 3 – 3x) = -y(x)

Отсюда следует, что функция является нечетной.

4) Функция непериодична.

5) Найдем промежутки монотонности и точки экстремума функции: y’ = 3x 2 - 3.

Критические точки: 3x 2 – 3 = 0, x 2 =1, x= ±1.

y(-1) = (-1) 3 – 3(-1) = 2

y(1) = 1 3 – 3*1 = -2

6) Найдем промежутки выпуклости и точки перегиба функции: y’’ = 6x

Критические точки: 6x = 0, x = 0.

y(0) = 0 3 – 3*0 = 0

7) Функция непрерывна, асимптот у нее нет.

8) По результатам исследования построим график функции.

Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R .Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента x , при которых функция y = f (x )определена, называется областью определения функции . Множество Y всех действительных значений y , которые принимает функция, называетсяобластью значений функции . Теперь можно дать более точное определение функции: правило (закон) соответствия между множествами X и Y , по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией .

Из этого определения следует, что функция считается заданной, если:

Задана область определения функции X ;

Задана область значений функции Y ;

Известно правило (закон) соответствия, причём такое, что для каждого

Значения аргумента может быть найдено только одно значение функции.

Это требование однозначности функции является обязательным.

Монотонная функция. Если для любых двух значений аргумента x 1 и x 2 из условия x 2 > x 1 следует f (x 2) > f (x 1), то функция f ( x ) называетсявозрастающей ; если для любых x 1 и x 2 из условия x 2 > x 1 следует f ( x 2) < f ( x 1), то функция f ( x ) называется убывающей . Функция, которая только возрастает или только убывает, называется монотонной .

Ограниченная и неограниченная функции. Функция называется ограниченной , если существует такое положительное число M , что | f (x ) | M для всех значений x . Если такого числа не существует, то функция - неограниченная .

П р и м е р ы.

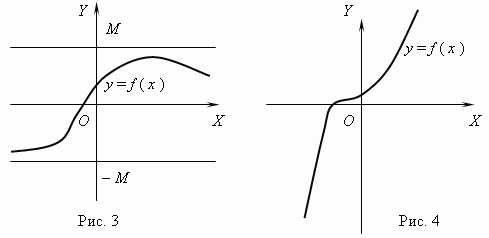
Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 - как раз наоборот, монотонная, но неограниченная. (Объясните это, пожалуйста!).

Непрерывная и разрывная функции. Функция y = f (x ) называется непрерывной в точке x = a , если:

1) функция определена при x = a , т.e. f (a ) существует;

2) существует конечный предел lim f (x ) ;

x →a

(см. «Пределы функций»)

3) f (a ) = lim f (x ) .

x →a

Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a .

Если функция непрерывна во всех точках своей области определения , то она называется непрерывной функцией .

Чётная и нечётная функции. Если для любого x f (- x ) = f (x ), то функция называется чётной ;если же имеет место: f (- x ) = - f (x ), то функция называется нечётной . График чётной функции симетричен относительно оси Y (рис.5), a график нечётной функции сим метричен относительно начала координат (рис.6).

Периодическая функция. Функция f (x ) - периодическая , если существует такое отличное от нуля число T , что для любого x из области определения функции имеет место: f (x + T ) = f (x ). Такое наименьшее число называется периодом функции . Все тригонометрические функции являются периодическими.

П р и м е р 1 . Доказать, что sin x имеет период 2 .

Р е ш е н и е. Мы знаем, что sin (x+ 2n ) = sin x , где n = 0, ± 1, ± 2, …

Следовательно, добавление 2n к аргументу синуса не

Меняет его значениe. Существует ли другое число с таким

Же свойством?

Предположим, что P - такое число, т.e. равенство:

Sin (x+ P ) = sin x ,

Справедливо для любого значения x . Но тогда оно имеет

Место и при x = / 2 , т.e.

Sin ( / 2 + P ) = sin / 2 = 1.

Но по формуле приведения sin ( / 2 + P ) = cos P . Тогда

Из двух последних равенств следует, что cos P = 1, но мы

Знаем, что это верно лишь при P = 2n . Так как наименьшим

Отличным от нуля числом из 2n является 2, то это число

И есть период sin x . Аналогично доказывается, что 2 из n есть , таким образом, это период sin 2x .

Нули функции. Значение аргумента, при котором функция равна 0, называется нулём ( корнем) функции . Функция может иметь несколько нулей.Например, функция y = x (x + 1) (x -3) имеет три нуля: x = 0, x = -1, x = 3. Геометрически нуль функции - это абсцисса точки пересечения графика функции с осью Х .

На рис.7 представлен график функции с нулями: x = a , x = b и x = c .

Асимптота. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой .

Для понимая данной темы, рассмотрим функцию, изображенную на графике // Покажем, как график функции позволяет определить ее свойства.

Разбираем свойства функции на примере

Областью определения функции явл. промежуток [ 3,5; 5,5].

Областью значений функции явл. промежуток [ 1; 3].

1. При x = -3, x =- 1, x = 1,5, х=4,5 значение функции равно нулю.

Значение аргумента, при котором значение функции равно нулю, называют нулем функции.

//т.е. для данной функции числа -3;-1;1,5; 4,5 являются нулями.

2. На промежутках [ 4,5; 3) и (1; 1,5) и (4,5;5,5] график функции f расположен над осью абсцисс, а на промежутках (-3; -1) и (1,5; 4,5) под осью абсцисс, это объясняется так -на промежутках [ 4,5; 3) и (1; 1,5) и (4,5;5,5] функция принимает положительные значения, а на промежутках (-3; -1) и (1,5; 4,5) отрицательные.

Каждый из указанных промежутков (там где функция принимает значения одного и того же знака) называют промежутком знакопостоянства функции f.//т.е. например, если взять промежуток (0; 3), то он не является промежутком знакопостоянства данной функции.

В математике принято при поиске промежутков знакопостоянства функции указывать промежутки максимальной длины. //Т.е. промежуток (2; 3) является промежутком знакопостоянства функции f, но в ответ следует включить промежуток [ 4,5; 3), содержащий промежуток (2; 3).

3. Если перемещаться по оси абсцисс от 4,5 до 2, то можно заметить, что график функции идет вниз, то есть значения функции уменьшаются. //В математике принято говорить, что на промежутке [ 4,5; 2] функция убывает.

С увеличением x от 2 до 0 график функции идет вверх, т.е. значения функции увеличиваются. //В математике принято говорить, что на промежутке [ 2; 0] функция возрастает.

Функцию f называют , если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что x2 > x1, выполняется неравенство f (x2) > f (x1). // или Функцию называют возрастающей на некотором промежутке , если для любых значений аргумента из этого промежутка большему значению аргумента соответствует большее значение функции.//т.е. чем больше х, тем больше у.

Функцию f называют убывающей на некотором промежутке , если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что x2 > x1, выполняется неравенство f(x2)убывающей на некотором промежутке, если для любых значений аргумента из этого промежутка большему значению аргумента соответствует меньшее значение функции. //т.е. чем больше х, тем меньше у.

Если функция возрастает на всей области определения, то ее называют возрастающей .

Если функция убывает на всей области определения, то ее называют убывающей .

Пример 1. график возрастающей и убывающей функций соотвественно.

Пример 2.

Определить явл. ли линейная функция f (x) = 3x + 5 возрастающей или убывающей?

Доказательство. Воспрользуемся определениями. Пусть х1 и x2 произвольные значения аргумента, причем x1 < x2., например х1=1, х2=7

Русская гимназия

КОНСПЕКТ

Выполнил

ученик 10“Ф” класса Бурмистров Сергей

Руководитель

учитель Математики

Юлина О.А.

Нижний Новгород

Функция и её свойства

Функция- зависимость переменной у от переменной x , если каждому значению х соответствует единственное значение у .

Переменная х- независимая переменная или аргумент.

Переменная у- зависимая переменная

Значение функции- значение у , соответствующее заданному значению х .

Область определения функции- все значения, которые принимает независимая переменная.

Область значений функции (множество значений)- все значения, которые принимает функция.

Функция является четной- если для любого х f(x)=f(-x)

Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x)

Возрастающая функция- если для любых х 1 и х 2 , таких, что х 1 < х 2 , выполняется неравенство f( х 1 ) х 2 )